监督学习
本章继续研究监督学习的问题。
1 回归问题
我们随机制造一个样本空间\({x _2} \geqslant 2{x _1} + 1\),对于对空间进行分类。具体例子如下:
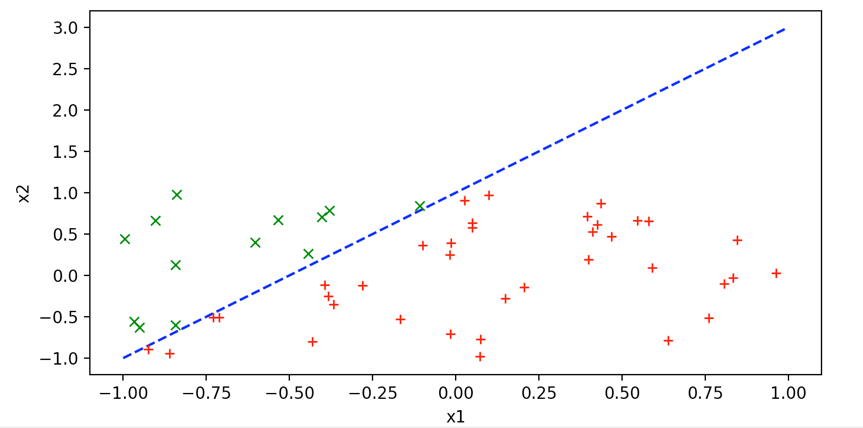
对于这些样本,假定可以通过二维线性曲线进行分类。然后模拟出某条曲线,使样本得到一个很好的分类。
这个分类问题的样本的y值只有0或1(0-1分布或伯努利分布),即表示在直线上面或直线下面。如果用之前的线性回归结果将非常糟糕。因为对于分类问题,线性回归得到的线性曲线,得到的\(y > 1\)或\(y < 0\)这些是没有意义的,肯定是错误的。因此引入了logistic函数,转换为Logistic regression,logistic函数如下:
$$h(z) = \frac{1}{{1 + {e^{ - z}}}}$$函数曲线如下:
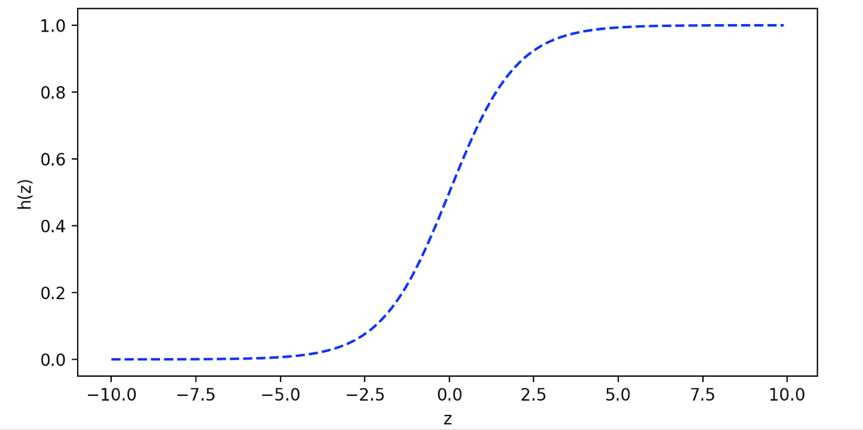
如果我们设置\(z = {\theta _1}{x _1} + {\theta _0} - {x _2}\)。因此,对于分类问题就可以转化为:对于\({x _2} \geqslant {\theta _1}{x _1} + {\theta _0}\)就可以转化为h(z)趋向于0的程度,对于\({x _2} \leqslant {\theta _1}{x _1} + {\theta _0}\)就可以转化为h(z)趋向于1的程度。我们简化为如下公式:
$$z = {\theta _1}{x _1} + {\theta _0}{x _0} + {\theta _2}{x _2} = {\theta ^T}x$$其中,\({x _0} = 1\),\({\theta _2} = - 1\)。
2 回归问题推导
我们求辅助函数的导数,以备后来使用:
$$h'(z) = (\frac{1}{{1 + {e^{ - z}}}})' = - \frac{{ - {e^{ - z}}}}{{{{(1 + {e^{ - z}})}^2}}} = \frac{1}{{1 + {e^{ - z}}}}(1 - 1 + {e^{ - z}}) = h(z)(1 - h(z))$$接下来我们从公式角度对问题进行建模分析与推导。
这里我们将我们的函数\({h_\theta }(x)\)转化为如下形式:
$${h_\theta }(x) = \frac{1}{{1 + {e^{ - {\theta ^T}x}}}}$$对于0-1分布,由于\({h_\theta }(x)\)只能为0或1。所以,在已知\(x\)和\({\theta}\)的情况下,我们可以认为有\({h_\theta }(x)\)的概率得到\(y=1\)。因此有如下公式:
$$p(y = 1|x,\theta ) = {h_\theta }(x)$$ $$p(y = 0|x,\theta ) = 1 - {h_\theta }(x)$$综合两个公式有如下公式:
$$p(y|x,\theta ) = {h_\theta }{(x)^y}{(1 - {h _\theta }(x))^{(1 - y)}}$$即在已经样本的情况下得到准确的\(y\),即要使用极大释然方法,得到样本概率乘积的最大值,即得到下式的最大值:
$$L(\theta ) = \prod\limits _{i = 1}^m {{h _\theta }{{(x{}^i)}^{{y^i}}}{{(1 - {h _\theta }({x^i}))}^{(1 - {y^i})}}} $$取自然对数,对其中一个维度\({\theta _j}\)求偏导数,如下:
$$\ell ({\theta _j}) = \frac{{\partial \ln (L(\theta ))}}{{\partial {\theta _j}}} = \frac{\partial } {{\partial {\theta _j}}}(\sum\limits _{i = 1}^m {({y^i}\ln ({h _\theta }(x{}^i)) + (1 - {y^i})} \ln (1 - {h _\theta }(x{}^i))))$$我们使用一个辅助函数\(z = {\theta ^T}x\), 并且\(\ln x\)的倒数是\(\frac{1}{x}\)。
又由于复合函数有如下求导法则:
其中\(z = g(x)\)。。(这里再次强调下标识维度,上表是样本编号)。所以有:
$$\ell ({\theta _j}) = \frac{{\partial L(\theta )}}{{\partial {\theta _j}}} = \frac{\partial }{{\partial {\theta _j}}}(\sum\limits _{i = 1}^m {({y^i}\ln ({h _\theta }(x{}^i)) + (1 - {y^i})} \ln (1 - {h _\theta }(x{}^i))))$$这里设\(z = {\theta ^T}x\),有:
$$\ell ({\theta _j}) = \sum\limits _{i = 1}^m {({y^i}\frac{1}{{h(z)}}h'(z) + (1 - {y^i})} \frac{1}{{1 - h(z)}}( - h'(z)))$$将之前的倒数公式带入其中,有:
$$\ell ({\theta _j}) = \sum\limits _{i = 1}^m {(x _j^i(y - {h _\theta }({x^i})))} $$因此这样就可以使用如下的式子学习样本值:
$${\theta _j} = {\theta _j} + \alpha \sum\limits _{i = 1}^m {(x _j^i(y - {h _\theta }({x^i})))} $$3 代码
从这一章开始讲代码从matlab转化更为通用的python。
我们选取合适的步长,当\(J({\theta})\)小于合适的阈值(这里配置为4),就认为迭代完成。分类代码如下:
import random
import math
import numpy as np
from matplotlib import pyplot as plt
k = 2
b = 1
x1_res = [-0.711, -0.2798, 0.4258, 0.4108, 0.0492, -0.842, -0.6036, -0.8394, 0.395, -0.8612, 0.806, 0.1476, 0.5464,
0.3992,
0.8326, 0.76, -0.7288, 0.0718, -0.4436, 0.8448, -0.017, -0.108, -0.4032, -0.9678, -0.4322, -0.9024, -0.0146,
-0.5346, -0.3808, 0.0498, 0.6376, -0.3946, 0.5896, -0.9504, 0.2046, -0.0994, 0.468, -0.9236, 0.0996, 0.4366,
-0.167, 0.9618, 0.5796, -0.383, 0.0254, -0.367, 0.0734, -0.8434, -0.9948, -0.0188]
x2_res = [-0.5108, -0.1254, 0.6166, 0.5296, 0.5758, -0.5972, 0.3994, 0.9808, 0.7134, -0.9414, -0.098, -0.2778, 0.667,
0.1916, -0.0298, -0.5124, -0.509, -0.9754, 0.261, 0.4256, -0.7104, 0.8398, 0.7094, -0.5558, -0.799, 0.666,
0.392,
0.6688, 0.7832, 0.6372, -0.788, -0.1138, 0.0922, -0.6254, -0.1456, 0.3608, 0.4694, -0.8946, 0.9708, 0.8736,
-0.5254, 0.0252, 0.6554, -0.2486, 0.9064, -0.35, -0.7724, 0.131, 0.4446, 0.2468]
def make_samples(x0_arr,x1_arr,x2_arr,y_arr):
# classified by x_2 = 2*x_1 + 1 . (x_1,x_2) is the point of 2-D plane
# y is 0 or 1, means 'x_2 >= 2*x_1 + 1 ' or 'x_2 < 2*x_1 + 1'
for i in range(len(x1_res)):
x0_arr.append(1)
x1_arr.append(x1_res[i])
x2_arr.append(x2_res[i])
y_arr.append(0 if (x2_arr[i] >= k * x1_arr[i] + b ) else 1)
def h(z):
return 1/(1 + math.exp(-1*z))
def h_xita(x0,x1,x2,xita):
return h(transvection([x0,x1,x2], xita))
def transvection(a,b):
return np.dot(a, b)
def J(x0_arr,x1_arr,x2_arr,y_arr,xita):
sum = 0;
length = len(x1_arr)
for i in range(length):
sum = sum + ( h_xita(x0_arr[i],x1_arr[i],x2_arr[i],xita) - y_arr[0] )**2
return sum/2
def updateXita(x0_arr,x1_arr,x2_arr,y_arr,xita,a,update_x):
sum = 0;
length = len(x0_arr)
for i in range(length):
sum = sum + ( y_arr[i] - h_xita(x0_arr[i],x1_arr[i],x2_arr[i],xita) ) * update_x[i]
return sum*a
def showPic(k,b,point_x1_arr,point_x2_arr):
## show line
X = np.arange(-1,1,0.001)
Y=[]
for i in range(X.size):
Y.append(k*X[i]+b)
plt.plot(X, Y, 'b--', label="logistic")
## show points
for i in range(len(point_x1_arr)):
if(point_x2_arr[i]>2*point_x1_arr[i]+1):
plt.plot(point_x1_arr[i],point_x2_arr[i],'b--',marker = 'x', color = 'g')
else:
plt.plot(point_x1_arr[i],point_x2_arr[i],'r--',marker = '+', color = 'r')
plt.xlabel("x1")
plt.ylabel("x2")
plt.figure(figsize=(8, 4))
plt.show()
if __name__== "__main__":
x0_arr = []
x1_arr = []
x2_arr = []
y_arr = []
make_samples(x0_arr,x1_arr,x2_arr,y_arr)
xita = [1,20,-1]
a = 0.01
limit = 4
count = 0
while 1:
j = J(x0_arr, x1_arr, x2_arr, y_arr, xita)
print("j=",j)
if j < limit:
break;
xita[0] = xita[0] + updateXita(x0_arr, x1_arr, x2_arr, y_arr, xita, a, x0_arr)
xita[1] = xita[1] + updateXita(x0_arr, x1_arr, x2_arr, y_arr, xita, a, x1_arr)
count = count + 1
print("cout=",count)
print("xita0=",xita[0]," xita1=",xita[1])
showPic(xita[1],xita[0],x1_arr,x2_arr)
print(xita)
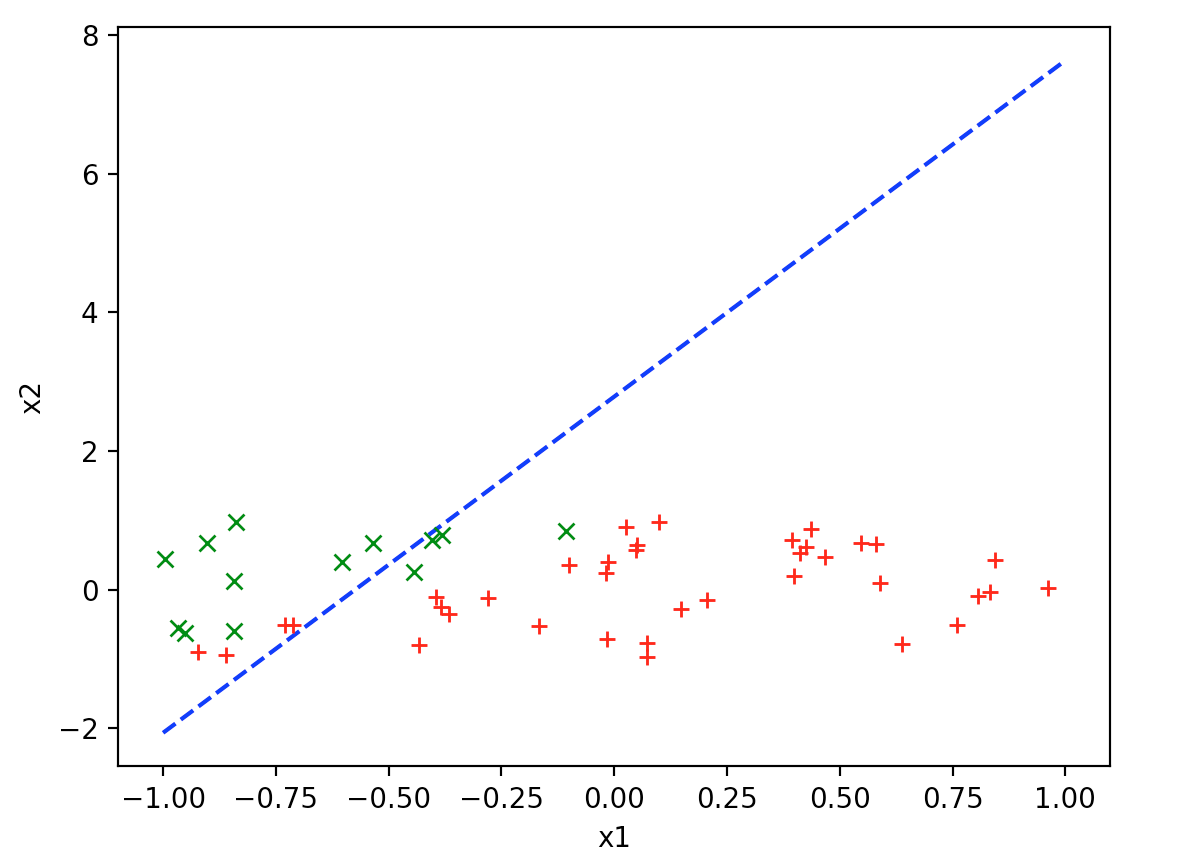
经过数论迭代分析,得到\( \theta _0 = 2.7841420917875297 \),\( \theta _1 = 4.850051144306185 \)。
得到如下结果:
4 代码的改进
经过试验发现上面的算法的问题是如果选取合适的阈值。这里将算法修改为两次的\(J({\theta})\)的差值小于0.00001,这样就任务函数已经几近收敛,然后结束迭代。另外,如果\(J({\theta})\)的值某一次迭代增大了,说明算法异常或者迭代参数设置过大。修改后的代码如下:
while 1:
j = J(x0_arr, x1_arr, x2_arr, y_arr, xita)
print("j=",j)
if j > j_last:
print("算法异常或选取迭代系数过大")
break;
if j_last - j < 0.00001:
print("out ",j_last - j)
break;
j_last = j
xita[0] = xita[0] + updateXita(x0_arr, x1_arr, x2_arr, y_arr, xita, a, x0_arr)
xita[1] = xita[1] + updateXita(x0_arr, x1_arr, x2_arr, y_arr, xita, a, x1_arr)
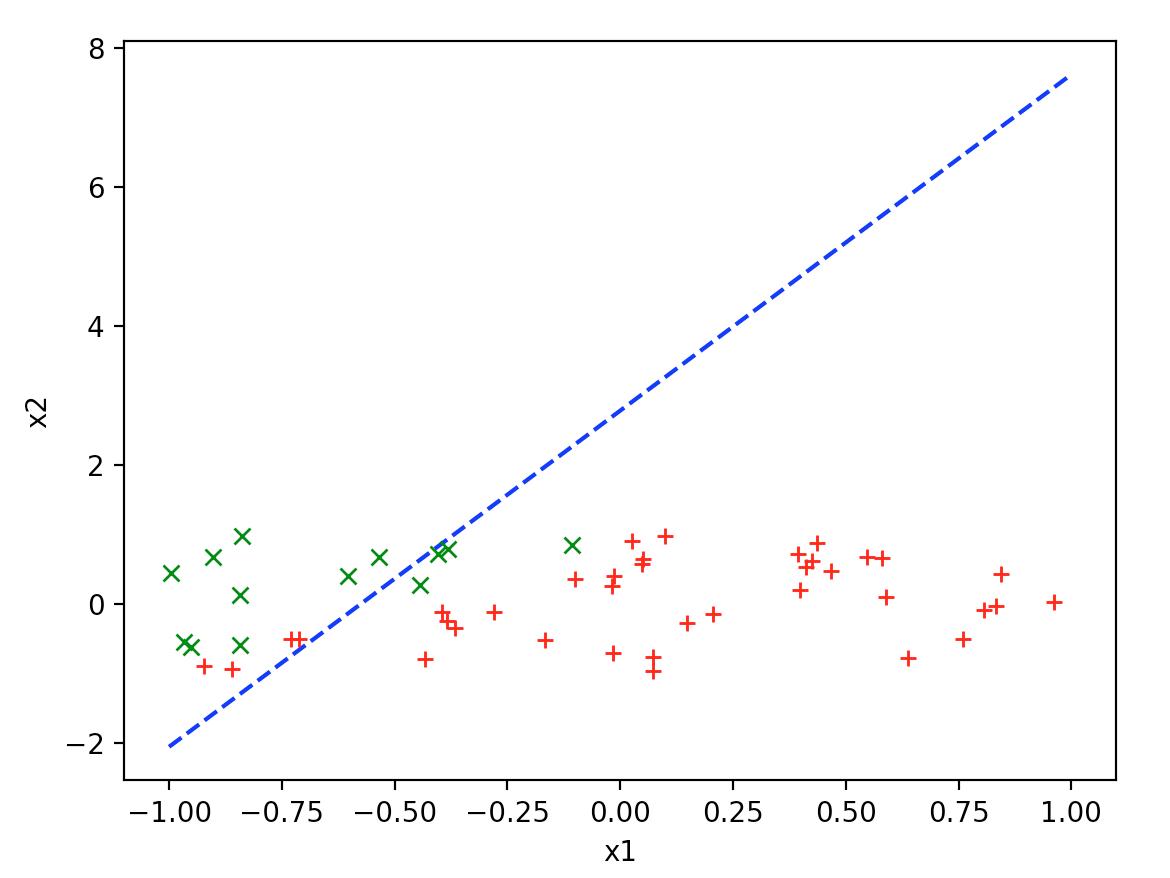
得到如下结果:
5 牛顿法改进
这里说明另外一种快速求值的方法,牛顿法。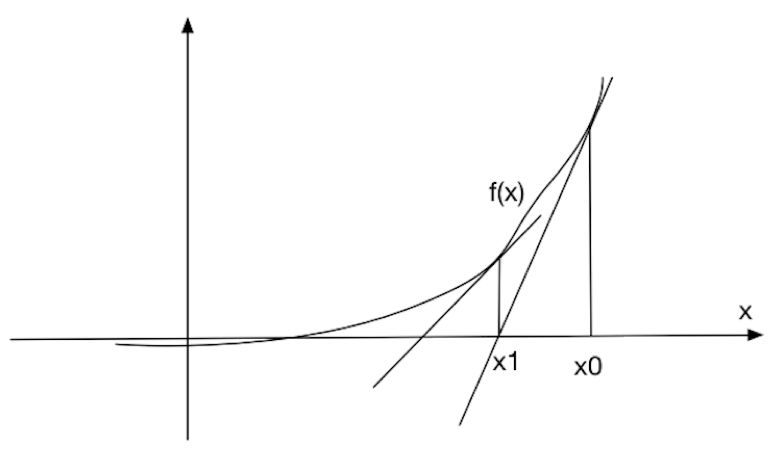
如上所示为牛顿法的简易过程。我们初始值为\(x _0\),然后在\((x _0,f(x _0))\)做切线得到\(x _0\),依次类推会接近于得到\(x _n\),使得\(f(x _n)\)接近于0。具体算法的证明请见文献2。
根据上面的算法,我们可以轻易的推导出
$${x _{i + 1}} = {x _i} - \frac{{f({x _i})}}{{f'({x _i})}}$$联系之前的问题,我们可以转化快速得到\({\theta _j}\)使得\(\ell ({\theta _j}) = 0\)问题。(注: 之前的算法使找到最优下降方向使得\(J({\theta})\)最小,而牛顿法是直接得到最优的\({\theta _j}\))
本问题的公式如下:
$$\ell ({\theta _j}) = \sum\limits _{i = 1}^m {(x _j^i(y - {h _\theta }({x^i})))} $$ $$\ell '({\theta _j}) = - \sum\limits _{i = 1}^m {{{(x _j^i)}^2}} $$ $${\theta _j}: = {\theta _j} - \frac{{\ell ({\theta _j})}}{{\ell '({\theta _j})}} = {\theta _j} - \frac{{\sum\limits _{i = 1}^m {(x _j^i(y - {h _\theta }({x^i})))} }}{{ - \sum\limits _{i = 1}^m {{{(x _j^i)}^2}} }}$$代码如下:
import sys
import math
import numpy as np
from matplotlib import pyplot as plt
k = 2
b = 1
x1_res = [-0.711, -0.2798, 0.4258, 0.4108, 0.0492, -0.842, -0.6036, -0.8394, 0.395, -0.8612, 0.806, 0.1476, 0.5464,
0.3992,
0.8326, 0.76, -0.7288, 0.0718, -0.4436, 0.8448, -0.017, -0.108, -0.4032, -0.9678, -0.4322, -0.9024, -0.0146,
-0.5346, -0.3808, 0.0498, 0.6376, -0.3946, 0.5896, -0.9504, 0.2046, -0.0994, 0.468, -0.9236, 0.0996, 0.4366,
-0.167, 0.9618, 0.5796, -0.383, 0.0254, -0.367, 0.0734, -0.8434, -0.9948, -0.0188]
x2_res = [-0.5108, -0.1254, 0.6166, 0.5296, 0.5758, -0.5972, 0.3994, 0.9808, 0.7134, -0.9414, -0.098, -0.2778, 0.667,
0.1916, -0.0298, -0.5124, -0.509, -0.9754, 0.261, 0.4256, -0.7104, 0.8398, 0.7094, -0.5558, -0.799, 0.666,
0.392,
0.6688, 0.7832, 0.6372, -0.788, -0.1138, 0.0922, -0.6254, -0.1456, 0.3608, 0.4694, -0.8946, 0.9708, 0.8736,
-0.5254, 0.0252, 0.6554, -0.2486, 0.9064, -0.35, -0.7724, 0.131, 0.4446, 0.2468]
def make_samples(x0_arr,x1_arr,x2_arr,y_arr):
# classified by x_2 = 2*x_1 + 1 . (x_1,x_2) is the point of 2-D plane
# y is 0 or 1, means 'x_2 >= 2*x_1 + 1 ' or 'x_2 < 2*x_1 + 1'
for i in range(len(x1_res)):
x0_arr.append(1)
x1_arr.append(x1_res[i])
x2_arr.append(x2_res[i])
y_arr.append(0 if (x2_arr[i] >= k * x1_arr[i] + b ) else 1)
def h(z):
return 1/(1 + math.exp(-1*z))
def h_xita(x0,x1,x2,xita):
return h(transvection([x0,x1,x2], xita))
def transvection(a,b):
return np.dot(a, b)
def l(x0_arr,x1_arr,x2_arr,y_arr,xita,a,update_x):
sum = 0;
for i in range(len(x0_arr)):
sum = sum + ( y_arr[i] - h_xita(x0_arr[i],x1_arr[i],x2_arr[i],xita) ) * update_x[i]
return sum*a
def derl(update_x):
sum = 0;
for i in range(len(update_x)):
sum = sum + update_x[i]*update_x[i];
return -1 * sum
def showPic(k,b,point_x1_arr,point_x2_arr):
## show line
X = np.arange(-1,1,0.001)
Y=[]
for i in range(X.size):
Y.append(k*X[i]+b)
plt.plot(X, Y, 'b--', label="logistic")
## show points
for i in range(len(point_x1_arr)):
if(point_x2_arr[i]>2*point_x1_arr[i]+1):
plt.plot(point_x1_arr[i],point_x2_arr[i],'b--',marker = 'x', color = 'g')
else:
plt.plot(point_x1_arr[i],point_x2_arr[i],'r--',marker = '+', color = 'r')
plt.xlabel("x1")
plt.ylabel("x2")
plt.figure(figsize=(8, 4))
plt.show()
if __name__== "__main__":
x0_arr = []
x1_arr = []
x2_arr = []
y_arr = []
make_samples(x0_arr,x1_arr,x2_arr,y_arr)
xita = [1,20,-1]
xita_bak = [10000,10000]
count = 0
while 1:
xita[0] = xita[0] - l(x0_arr, x1_arr, x2_arr, y_arr, xita, 1,x0_arr)/derl(x0_arr)
xita[1] = xita[1] - l(x0_arr, x1_arr, x2_arr, y_arr, xita, 1, x1_arr) / derl(x1_arr)
if abs(l(x0_arr, x1_arr, x2_arr, y_arr, xita, 1,x0_arr)) <= 0.001 :
print("xita = ",xita)
break;
xita_bak[1]=xita[1]
xita_bak[0]=xita[0]
count = count + 1
print("count=", count, " xita = ", xita)
showPic(xita[1],xita[0],x1_arr,x2_arr)
print(xita)
得到\({\theta _0}\)和\({\theta _1}\)分别为
2.7762287194293407, 4.835356147838368。得到的曲线如下:
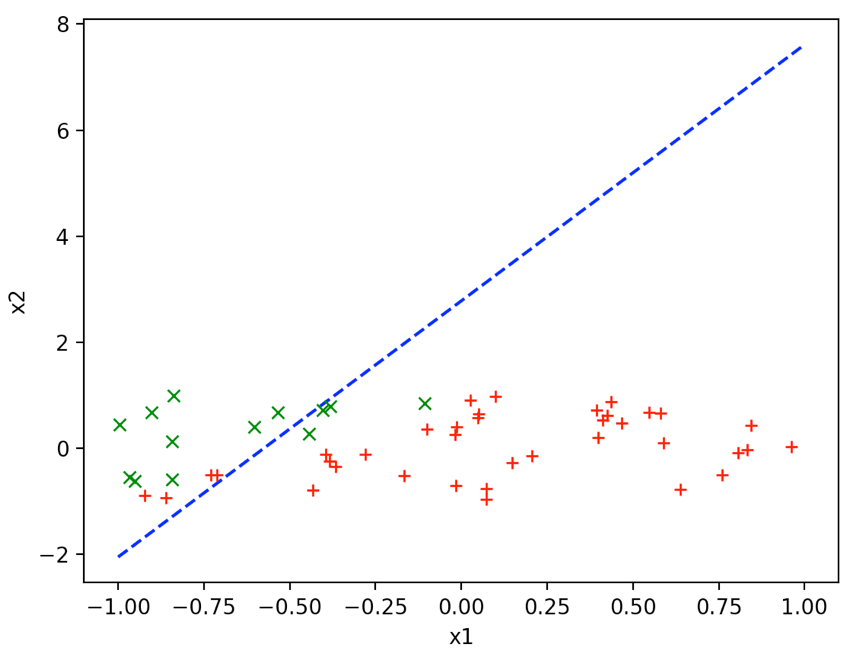
6 参考文献
- 1 << cs229-notes1 >>
- 2 << 计算机科学计算 >> 施吉林,张宏伟,金光日编