Softmax Regression
下面介绍一下指数族分布的另外一个例子。之前的逻辑回归中,可以用来解决二分类的问题。对于有k中可能结果的时候,问题就转化为多分类问题了,也就是接下来要说明的softmax regression问题。
s
1 函数定义
在进行下一步推导前,我们先定义部分辅助函数。我们这里事先定义一个k-1维向量\(T(y)\),这里具体对应于指数族分布的\(T(y)\),具体定义如下:
$$T(1) = \left[ \begin{gathered} 1 \hfill \\\ 0 \hfill \\\ 0 \hfill \\\ ... \hfill \\\ 0 \hfill \\ \end{gathered} \right],T(2) = \left[ \begin{gathered} 0 \hfill \\\ 1 \hfill \\\ 0 \hfill \\\ ... \hfill \\\ 0 \hfill \\ \end{gathered} \right],T(3) = \left[ \begin{gathered} 0 \hfill \\\ 0 \hfill \\\ 1 \hfill \\\ ... \hfill \\\ 0 \hfill \\\ \end{gathered} \right],...,T(k - 1) = \left[ \begin{gathered} 0 \hfill \\\ 0 \hfill \\\ 0 \hfill \\\ ... \hfill \\\ 1 \hfill \\ \end{gathered} \right],T(k) = \left[ \begin{gathered} 0 \hfill \\\ 0 \hfill \\\ 0 \hfill \\\ ... \hfill \\\ 0 \hfill \\ \end{gathered} \right]$$我们定义\(T(y) _1\)表示的\(T(y)\)第一个元素,其他依次类推。
然后再引入一个函数,具体定义如下:
$$1\{ true\} = 1$$ $$1\{ false\} = 0$$可以通过带入值的方式验证上式。
2 模型推导
在softmax中,我们知道\(y \in \{ 1,2,…,k\}\)。我们设置\(y=1\)的概率为\(\phi _1\),
类似的有\(y=k\)的概率为\(\phi _k\),并且我们轻易得到如下公式:
由于我们已经知道\(p(y = i) = {\phi _i}\),综上可以得到:
$$p(y) = \phi _1^{1\{ y = 1\} }\phi _2^{1\{ y = 2\} }...\phi _k^{1\{ y = k\} } = \phi _1^{1\{ y = 1\} }\phi _2^{1\{ y = 2\} }...\phi _k^{1 - \sum\limits _{i = 1}^{k - 1} {1\{ y = i\} } } = \phi _1^{T{(y)} _1}\phi _2^{T{{(y)} _2}}...\phi _k^{1 - \sum\limits _{i = 1}^{k - 1} {T{(y)} _i} }$$ $$p(y) = \exp (T{(y) _1}\ln {\phi _1} + T{(y) _2}\ln {\phi _2} + ... + (1 - \sum\limits _{i = 1}^{k - 1} {T{{(y)} _i}} )\ln {\phi _k})$$ $$p(y) = \exp (T{(y) _1}\ln \frac{\phi _1}{\phi _k} + T{(y) _2}\ln \frac{\phi _2}{\phi _k} + ... + T{(y) _{k - 1}}\ln \frac{\phi _{k - 1}}{\phi _k} + \ln {\phi _k})$$我们对照指数族分布,其中\(T(y)\)我们已经定义,可以得到其他参数如下:
$$b(y) = 1$$ $$a(\eta ) = - \ln {\phi _k}$$ $$\eta = \left[ \begin{gathered} \ln \frac{\phi _1}{\phi _k} \hfill \\\ \ln \frac{\phi _2}{\phi _k} \hfill \\\ ... \hfill \\\ \ln \frac{\phi _{k - 1}}{\phi _k} \hfill \\\ \end{gathered} \right]$$我们用\(\eta\)来表示\(\phi\),目标是将我们的问题归整为一个变量的问题,从而更容易计算。对上面向量拆开计算得到:
$${\eta _i} = \ln \frac{\phi _i}{\phi _k}$$继而可以转化为:
$${\eta _i} = \ln \frac{\phi _i}{\phi _k}$$又由于我们已知\(\sum\limits _{j = 1}^k {\phi _j} = 1\),所以有:
$$\sum\limits _{i = 1}^k {e^{\eta _i}{\phi _k}} = 1$$继而有:
$${\phi _k} = \frac{1}{\sum\limits _{j = 1}^k {e^{\eta _j}}}$$最后我们可以得到:
$${\phi _i} = \frac{e^{\eta _i}}{\sum\limits _{j = 1}^k {e^{\eta _j}}}$$由于指数组分布假设是关于输入的线性函数,所以得到在已知\(x\)和\(\theta\)的情况下\(y=i\)的概率的公式,如下:
$$p(y = i|x,\theta ) = {\phi _i} = \frac{e^{\eta _i}}{\sum\limits _{j = 1}^k {e^{\eta _j}}} = \frac{e^{\theta _i^Tx}}{\sum\limits _{j = 1}^k {e^{\theta _j^Tx}}}$$这里我们可以得到\({h_\theta }(x)\),如下:
$${h_\theta }(x) = E[T(y)|x,\theta ] = E[\left( \begin{gathered} 1\{ y = 1\} \hfill \\\ 1\{ y = 2\} \hfill \\\ ... \hfill \\\ 1\{ y = k - 1\} \hfill \\\ \end{gathered} \right)|x,\theta ]$$ $${h_ \theta }(x) = E[\left( \begin{gathered} {\phi _1} \hfill \\\ {\phi _2} \hfill \\\ ... \hfill \\\ {\phi _{k - 1}} \hfill \\\ \end{gathered} \right)|x,\theta ] = \left( \begin{gathered} \frac{e^{\theta _1^Tx}}{\sum\limits _{j = 1}^k {e^{\theta _j^Tx}}} \hfill \\\ \frac{e^{\theta _2^Tx}}{\sum\limits _{j = 1}^k {e^{\theta _j^Tx}}} \hfill \\\ ... \hfill \\\ \frac{e^{\theta _{k - 1}^Tx}}{\sum\limits _{j = 1}^k {e^{\theta _j^Tx}}} \hfill \\\ \end{gathered} \right)$$其中,\(k\)为取值的可能集合的大小,\(\theta\)为一个\(k*n\)的矩阵。
到这里我们可以定义我们的损失函数了,如下:
$$J(x) = \frac{1}{2}\sum\limits _{i = 1}^m {{(T(y) - {h _\theta }(x))}^2}$$上式是一个向量,我们可以对这个向量继续求平方和,来衡量准确度,如下:
$$J(x) = \frac{1}{2}\sum\limits _{i = 1}^m {|{{(T(y) - {h _\theta }(x))}^2}|}$$损失函数已经定义完成,我们就有了算法的截止条件了。接下来就是找到算法的最优迭代方向,也就是计算其偏导数了。
我们使用最大释然性来计算迭代方向。建模的原则是:对于一个已知\(y=i\)的样本\((x,y)\),我们需要找到一个方向去迭代\(\theta\),使得\(\phi _i\)尽可能大,使得其他\(\phi\)尽可能小。当然由于所有\(\phi\)之和为1,所以我们只需要保证\(\phi _i\)尽可能大即可。因此,在已经的\(m\)个样本的情况下,我们只需要保证下面的式子最大:
$$\sum\limits _{i = 1}^m {p(y = {y^i}|x,\theta )} = \sum\limits _{i = 1}^m {\prod\limits _{l = 1}^k {p{(y = l|x,\theta )}^{1\{ {y^i} = l\}}} }$$取自然对数后,我们定义最大似然函数:
$$l(\theta ) = \sum\limits _{i = 1}^m {\ln \prod\limits _{l = 1}^k {(\frac{e^{\theta _l^Tx}}{\sum\limits _{j = 1}^k {e^{\theta _j^Tx}}})^{1\{{y^i} = l\}}}}$$当且仅当\({y^i} = l\)的时候, \(^{1{y^i=l\} = 1})。其他值为0,我们可以将连乘转化,如下:
$$l(\theta ) = \sum\limits _{i = 1}^m {\ln (\frac{e^{\theta _{y^i}^Tx}}{\sum\limits _{j = 1}^k {e^{\theta _j^Tx}}})} = \sum\limits _{i = 1}^m {\ln [\theta _{y^i}^Tx - \ln \sum\limits _{j = 1}^k {e^{\theta _j^Tx}}]} $$然后对其求偏导数,对\(y _i=f\)的时候后有:
$$\frac{\partial l(\theta )}{\partial {\theta _f}} = \sum\limits _{i = 1}^m {\ln [{x _f} - \frac{e^{\theta _f^Tx}{x _f}}{\sum\limits _{j = 1}^k {e^{\theta _j^Tx}}}]}$$对\({y_i} \ne f\)的时候,有:
$$\frac{\partial l(\theta )}{\partial {\theta _f}} = \sum\limits _{i = 1}^m {\ln [0 - \frac{e^{\theta _f^Tx}{x _f}}{\sum\limits _{j = 1}^k {e^{\theta _j^Tx}}}]}$$综上,可以得到:
$$\frac{\partial l(\theta )}{\partial {\theta _f}} = \sum\limits _{i = 1}^m {\ln [1\{ {y^i} = f\} - \frac{e^{\theta _f^Tx}}{\sum\limits _{j = 1}^k {e^{\theta _j^Tx}}}]{x _f}} = \sum\limits _{i = 1}^m {\ln [1\{{y^i} = f\} - {\phi _f}]{x _f}}$$\(x _f\)是一个向量,因为公式一次迭代更新一个维度下的一组\(\theta\)。事实上,这里是一个向量求微分。如果我们对的某个元素\(\theta\)进行微分,我们依然能够得到这个公式。
3 实际问题的解决
我们随机制造一组数据,在\(2*2\)的空间内使用直线\({x _2} = 0.5*{x _1}\)和直线\({x _2} = -0.5*{x _1}+2\)具体的分类如下:
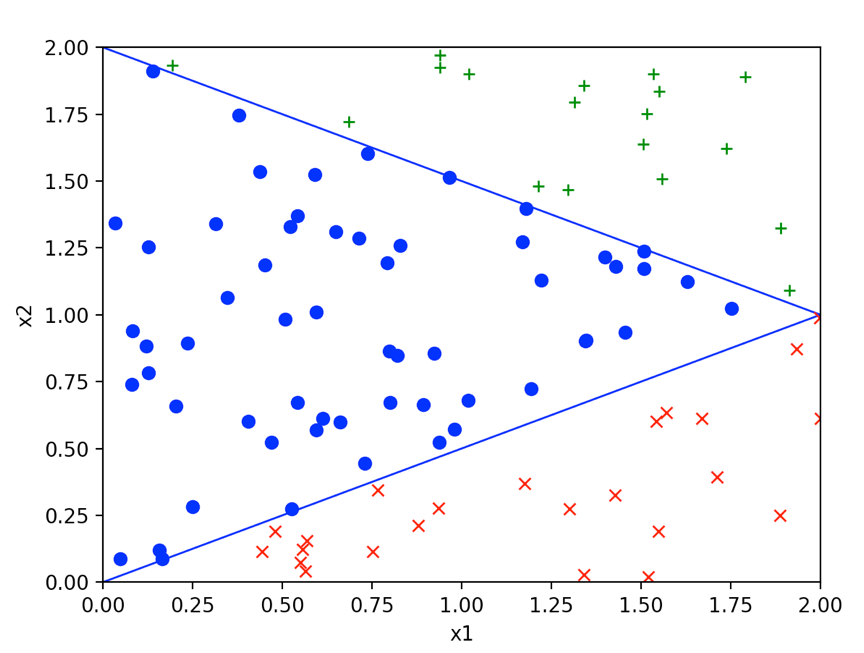
根据之前的推导,编写如下代码:
1 | import random |
经过33844次迭代之后,我们得到\(\theta\) = [[17.418683742474045, 13.989348587756815, -37.731307869980014],[-33.56035031194091, 1.3797244978249763, 34.095843086377855],[19.97548491920147, -11.65484983882828, 7.628008093823735]]
迭代的次数越多数据会越准确,这里迭代了上三万次,实际上可以通过牛顿法来减少迭代的次数,这里就不再重新代码了,牛顿法可以参见前面的文章。
然后,我们随机制造一组值,看看分类效果,具体如下:
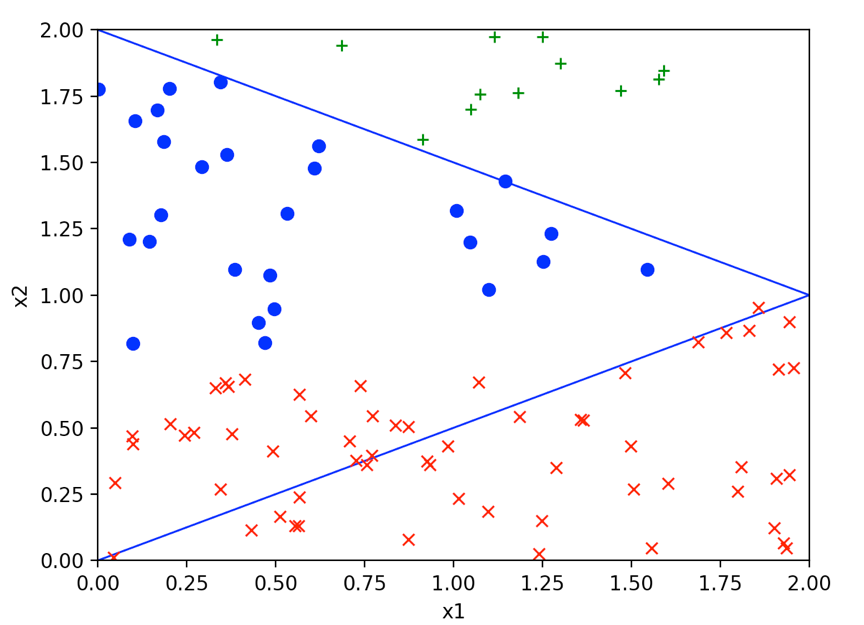
附录 公式推导手写版


