机器学习-2.5-监督学习之生成型学习算法

生成型学习算法

1 生成型学习算法简述

我们之前讲到的算法。譬如逻辑回归，试图从\(x\)直接学习得到一组映射关系到\(y\)，即通过样本\((x,y)\)学习得到,使得其能够准确的预测\(y\)。这类算法叫做判别性学习算法。

本节我们将介绍生成学习型算法。举个例子，对于一个大象，我们可以为大象构造一个关于其特征的模型。对于一条狗，同样可以为狗构造一个关于关于其特征的模型。对于一个新动物，我们可以根据前述构建的模型，判断这个动物是像大象多一点还是像狗多一点，来确定这动物是大象还是狗。

我们可以根据样本得到大象的特征模型\(p(x|y=0)\)和狗的特征模型\(p(x|y=1)\)，同时也可以得到\(p(y)\)。根据贝叶斯公式，有如下：

$$\max (p(y|x)) = \max (\frac{p(x|y)p(y)}{p(x)}) = \max (\frac{p(x|y)p(y)}{p(x|y = 1)p(y = 1) + p(x|y = 0)p(y = 0)})$$

对于我们做预测的时候，可以不考虑分母。

$$\max (p(y|x)) = \max (p(x|y)p(y))$$

为什么不考虑分母?我们可以将\(p(x|y)p(y)\)简化为\(f(y)\),因此分母就是\(f(1)+f(0)\)。如果我们通过样本对完成了建模，因此分母就是一个常数了，因此没有计算的必要了。

2 高斯判别分析

2.1 多维高斯分布介绍

略，详见cs229-note2.pdf

2.2 高斯判别分析模型

对于一个分类问题,\(y \in (0,1)\)。假设\(x\)是连续的随机变量，服从高斯分布。具体描述如下：

$$y \sim Bernoulli(\phi)$$ $$x|y = 0 \sim N({\mu _0},\Sigma)$$ $$x|y = 1 \sim N({\mu _1},\Sigma)$$ $$p(x|y = 0) = \frac{1}{{{(2\pi )}^{\frac{n}{2}}}|\Sigma {|^{\frac{n}{2}}}}\exp ( - \frac{1}{2}{(x - {\mu _0})^T}{\Sigma ^{ - 1}}(x - {\mu _0}))$$ $$p(x|y = 1) = \frac{1}{{{(2\pi )}^{\frac{n}{2}}}|\Sigma {|^{\frac{n}{2}}}}\exp ( - \frac{1}{2}{(x - {\mu _1})^T}{\Sigma ^{ - 1}}(x - {\mu _1}))$$

2.3 公式推导

我们设置\(\phi = p(y = 0)\)。根据前面的分析，在给定样本的情况下，我们需要保证下式最大。

$$\prod\limits _{i = 1}^m {p({y^i}|{x^i})} = \prod\limits _{i = 1}^m {p({x^i}|{y^i})p({y^i})}$$

这里为了简写，我们设置\({z _0} = x - {\mu _0}\) ，\({z _1} = x - {\mu _1}\)。取自然对数后，得到最大释然函数:

$$\ell ({\mu _1},{\mu _1},\Sigma ,\phi ) = \sum\limits _{i = 1}^m {\ln \{ {{[\frac{1}{{{{(2\pi )}^{\frac{n}{2}}}|\Sigma {|^{\frac{n}{2}}}}}\exp ( - \frac{1}{2}z _0^T{\Sigma ^{ - 1}}{z _0})]}^{1\{ {y^i} = 0\} }}{{[\frac{1}{{{{(2\pi )}^{\frac{n}{2}}}|\Sigma {|^{\frac{n}{2}}}}}\exp ( - \frac{1}{2}z _1^T{\Sigma ^{ - 1}}{z _1})]}^{1\{ {y^i} = 1\} }}\} } $$ $$\ell ({\mu _0},{\mu _1},\Sigma ,\phi ) = \sum\limits _{i = 1}^m {\{ 1\{ {y^i} = 0\} [ - \frac{1}{2}z _0^T{\Sigma ^{ - 1}}{z _0} - \frac{n}{2}\ln 2\pi - \frac{n}{2}\ln |\Sigma | + \ln \phi ] + 1\{ {y^i} = 1\} } [ - \frac{1}{2}z _1^T{\Sigma ^{ - 1}}{z _1} - \frac{n}{2}\ln 2\pi - \frac{n}{2}\ln |\Sigma | + \ln (1 - \phi )]\}$$

然后我们分别对各个参数求偏导数:

$$\frac{{\partial \ell ({\mu _0},{\mu _1},\sum ,\phi )}}{{\partial \phi }} = \sum\limits _{i = 1}^m {(\frac{{1\{ {y^i} = 1\} }}{\phi } - \frac{{1\{ {y^i} = 0\} }}{{1 - \phi }})} = \sum\limits _{i = 1}^n {(\frac{{1\{ {y^i} = 1\} }}{\phi } - \frac{{1 - 1\{ {y^i} = 1\} }}{{1 - \phi }})} = 0$$

所以有:

$$\phi = \frac{1}{m}\sum\limits _{i = 1}^n {1\{ {y^i} = 1\} }$$

然后对\(\mu _0\)求导：

$${\nabla _{{\mu _0}}}\ell ({\mu _0},{\mu _1},\Sigma ,\phi ) = \sum\limits _{i = 1}^m {{\nabla _{{\mu _0}}}( - \frac{1}{2}{{({x^i} - {\mu _0})}^T}{\Sigma ^{ - 1}}({x^i} - {\mu _0}))1\{ {y^i} = 0\} }$$ $${\nabla _{{\mu _0}}}\ell ({\mu _0},{\mu _1},\Sigma ,\phi ) = - \frac{1}{2}\sum\limits _{i = 1}^m {{\nabla _{{\mu _0}}}( - \mu _0^T{\Sigma ^{ - 1}}{x^i} - {{({x^i})}^T}{\Sigma ^{ - 1}}{\mu _0} + \mu _0^T{\Sigma ^{ - 1}}{\mu _0})1\{ {y^i} = 0\} }$$

我们对上面的式子分头计算。

\(\Sigma\)为对角阵。由于求偏微分的数为一个常数，因此该值与其迹的相同。另外，这里使用了一些关于迹的公式。具体详见附录。

$${\nabla _{{\mu _0}}}\mu _0^T{\Sigma ^{ - 1}}x = {\nabla _{{\mu _0}}}tr(\mu _0^T{\Sigma ^{ - 1}}{x^i}) = {[{\nabla _{\mu _0^T}}tr(\mu _0^T{\Sigma ^{ - 1}}{x^i})]^T} = {[{({\Sigma ^{ - 1}}{x^i})^T}]^T} = {\Sigma ^{ - 1}}{x^i}$$ $${\nabla _{{\mu _0}}}{({x^i})^T}{\Sigma ^{ - 1}}{\mu _0} = {\nabla _{{\mu _0}}}tr({({x^i})^T}{\Sigma ^{ - 1}}{\mu _0}) = {\nabla _{{\mu _0}}}{\mu _0}{({x^i})^T}{\Sigma ^{ - 1}} = {({({x^i})^T}{\Sigma ^{ - 1}})^T} = {\Sigma ^{ - 1}}{x^i}$$ $${\nabla _{{\mu _0}}}\mu _0^T{\Sigma ^{ - 1}}{\mu _0} = {[{\nabla _{\mu _0^T}}\mu _0^T{\Sigma ^{ - 1}}{\mu _0}E]^T} = [E\mu _0^T{\Sigma ^{ - 1}} + {E^T}\mu _0^T{({\Sigma ^{ - 1}})^T}] = 2{\Sigma ^{ - 1}}{\mu _0}$$

所以有:

$${\nabla _{{\mu _0}}}\ell ({\mu _0},{\mu _1},\Sigma ,\phi ) = - \sum\limits _{i = 1}^m {{\nabla _{{\mu _0}}}({\Sigma ^{ - 1}}{\mu _0} - {\Sigma ^{ - 1}}{x^i})1\{ {y^i} = 0\} } = 0$$ $${\mu _0} = \frac{{\sum\limits _{i = 1}^m {1\{ {y^i} = 0\} {x^i}} }}{{\sum\limits _{i = 1}^m {1\{ {y^i} = 0\} } }}$$

同理有:

$${\mu _1} = \frac{{\sum\limits _{i = 1}^m {1\{ {y^i} = 1\} {x^i}} }}{{\sum\limits _{i = 1}^m {1\{ {y^i} = 1\} } }}$$

然后对\(\Sigma^{-1}\)求偏导数。

$${\nabla _{{\Sigma ^{ - 1}}}}\ell ({\mu _0},{\mu _1},\Sigma ,\phi ) = \sum\limits _{i = 1}^m {{\nabla _{{\Sigma ^{ - 1}}}}[( - \frac{1}{2}z _0^T{\Sigma ^{ - 1}}{z _0} + \frac{1}{2}\ln \frac{1}{{|\Sigma |}})1\{ {y^i} = 0\} + ( - \frac{1}{2}z _1^T{\Sigma ^{ - 1}}{z _1} + \frac{1}{2}\ln \frac{1}{{|\Sigma |}})1\{ {y^i} = 1\} ]}$$

这里分开计算:

$${\nabla _{\Sigma ^{ - 1}}}(z _0^T{\Sigma ^{ - 1}}{z _0}) = {\nabla _{\sum ^{ - 1}}}tr(z _0^T{\Sigma ^{ - 1}}{z _0}) = {\nabla _{\sum ^{ - 1}}}tr({\Sigma ^{ - 1}}{z _0}z _0^T) = {({z _0}z _0^T)^T} = {z _0}z _0^T$$ $${\nabla _{\Sigma ^{ - 1}}}\ln \frac{1}{|\Sigma |} = {\nabla _{\Sigma ^{ - 1}}}\ln |{\Sigma ^{ - 1}}| = \frac{1}{|{\Sigma ^{ - 1}}|}{\nabla _{\Sigma ^{ - 1}}}{\Sigma ^{ - 1}} = {({({\Sigma ^{ - 1}})^{ - 1}})^T}$$

所以有:

$${\nabla _{{\sum ^{ - 1}}}}\ell ({\mu _0},{\mu _1},\Sigma ,\phi ) = \sum\limits _{i = 1}^m {[( - \frac{1}{2}{z _0}z _0^T + \frac{1}{2}\Sigma )1\{ {y^i} = 0\} + ( - \frac{1}{2}{z _1}z _1^T + \frac{1}{2}\Sigma )1\{ {y^i} = 1\} ]} = 0$$ $$\Sigma = \frac{1}{m}\sum\limits _{i = 1}^m {[({x^i} - {\mu _0}){{({x^i} - {\mu _0})}^T}1\{ {y^i} = 0\} + ({x^i} - {\mu _1}){{({x^i} - {\mu _1})}^T}1\{ {y^i} = 1\} ]}$$ $$\Sigma = \frac{1}{m}\sum\limits _{i = 1}^m {[({x^i} - {\mu _{{y^i}}}){{({x^i} - {\mu _{{y^i}}})}^T}]}$$

2.3 高斯型算法实例

我们分别以 \((1,1)\)和\((2,2)\)为均值生成一组高斯分布。下面图是生成的样本。

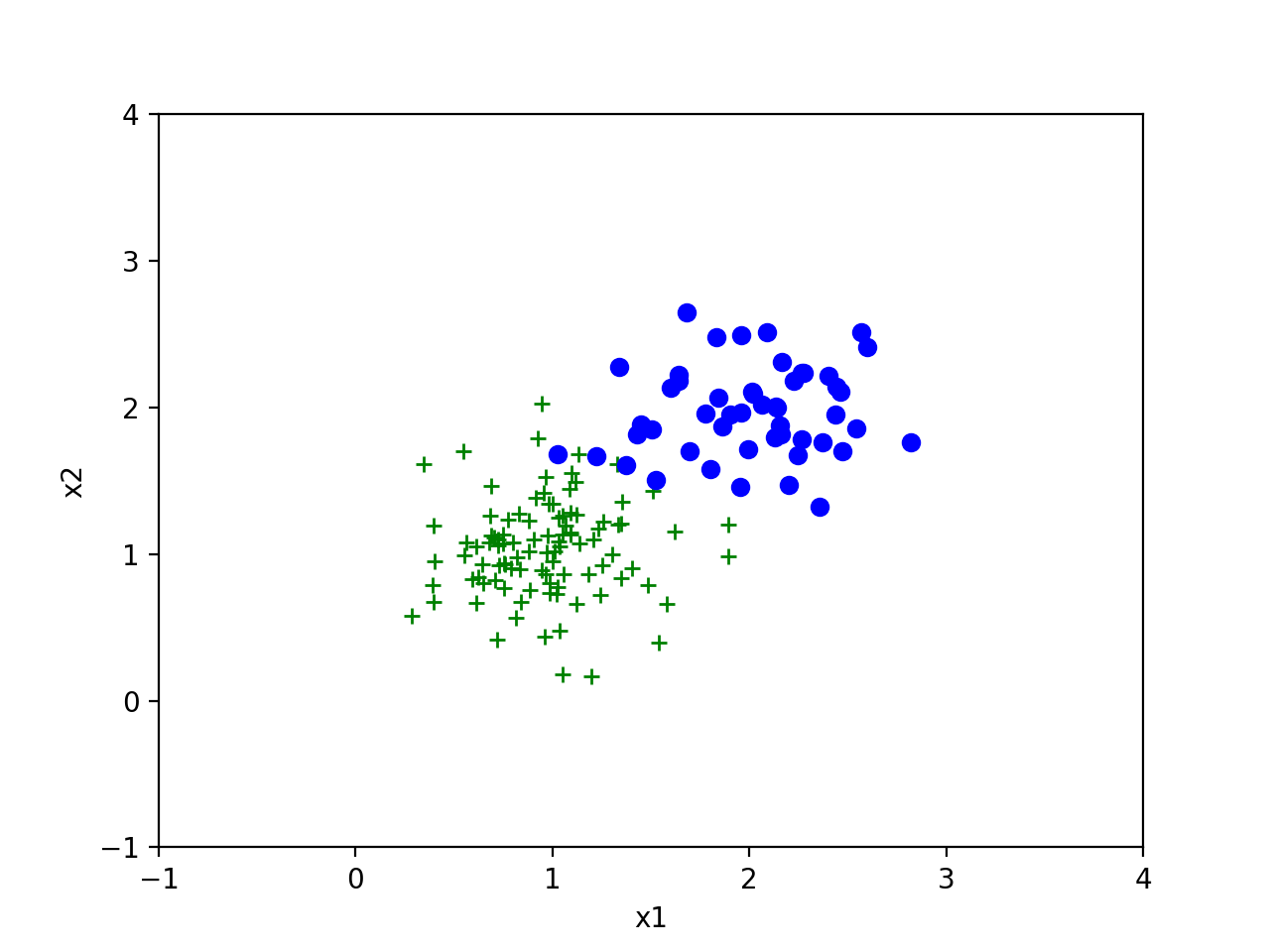
前提假设是我们知道两组分类是符合高斯分布的，切假定协方差相同。但我们不知道两组数据的均值和协方差。根据前面的公式有如下代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
import numpy as np
from matplotlib import pyplot as plt
from scipy.stats import multivariate_normal
import random
from matplotlib.lines import Line2D

## this is a program about GDA

global MAKE_DATA
global SHOW_PIC

def make_data(x):
  if MAKE_DATA == True:
    mean_1 = [1,1]
    mean_2 = [2,2]
    cov = [[0.1,0],[0,0.1]]
    arr1 = np.random.multivariate_normal(mean_1, cov, 100)
    arr2 = np.random.multivariate_normal(mean_2, cov, 50)
    print(arr1)
    print(arr2)
    x.append(arr1)
    x.append(arr2)
  if MAKE_DATA == False:
    arr1 = np.array([[ 0.88235916 , 1.01511634],[ 0.75243817 , 0.76520033],[ 0.95710848 , 1.41894337],[ 1.48682891 , 0.78885043],[ 1.24047011 , 0.71984948],[ 0.67611276 , 1.07909452],[ 1.03243669 , 1.08929695],[ 1.0296548  , 1.25023769],[ 1.54134008 , 0.39564824],[ 0.34645057 , 1.61499636],[ 0.77206174 , 1.23613698],[ 0.91446988 , 1.38537765],[ 0.99982962 , 1.34448471],[ 0.78745962 , 0.9046565 ],[ 0.74946602 , 1.07424473],[ 1.09294839 , 1.14711993],[ 0.39266844 , 0.78788004],[ 0.83112357 , 1.2762774 ],[ 1.05056188 , 1.13351562],[ 1.62101523 , 1.15035562],[ 0.70377517 , 1.1136416 ],[ 1.03715472 , 0.47905693],[ 0.94598381 , 0.8874837 ],[ 0.94447128 , 2.02796925],[ 0.72442242 , 1.09835206],[ 0.69046731 , 1.46232182],[ 1.20744606 , 1.10280041],[ 0.70665746 , 0.82139503],[ 1.08803887 , 1.4450361 ],[ 0.88530961 , 0.75727475],[ 0.98418545 , 0.80248161],[ 0.74970386 , 1.13205709],[ 0.72586454 , 1.06058385],[ 0.9071812  , 1.09975063],[ 0.75182835 , 0.93570147],[ 0.80052289 , 1.08168507],[ 0.40180652 , 0.9526211 ],[ 0.62312617 , 0.84385058],[ 0.68212516 , 1.25912717],[ 1.19773245 , 0.16399654],[ 0.96093132 , 0.43932091],[ 1.25471657 , 0.92371829],[ 1.12330272 , 1.26968747],[ 1.30361985 , 0.99862123],[ 1.23477665 , 1.1742804 ],[ 0.28471876 , 0.5806044 ],[ 1.89355099 , 1.19928671],[ 1.09081369 , 1.28467312],[ 1.40488635 , 0.90034427],[ 1.11672364 , 1.49070515],[ 1.35385212 , 1.35767891],[ 0.92746374 , 1.79096697],[ 1.89142562 , 0.98228303],[ 1.0555218  , 0.86070833],[ 0.69001255 , 1.12874741],[ 0.98137315 , 1.3398852 ],[ 1.02525371 , 0.77572865],[ 1.1354295  , 1.07098552],[ 1.50829164 , 1.43065998],[ 1.09928764 , 1.55540292],[ 0.64695084 , 0.79920395],[ 0.82059034 , 0.97533491],[ 0.56345455 , 1.08168272],[ 1.06673215 , 1.19448556],[ 0.96512548 , 1.5268577 ],[ 0.96914451 , 1.00902985],[ 0.72879413 , 0.92476415],[ 1.0931483  , 1.13572242],[ 1.34765121 , 0.83841006],[ 1.57813788 , 0.65915892],[ 0.59032608 , 0.82747946],[ 0.83838504 , 0.67588473],[ 1.35101322 , 1.21027851],[ 0.71762153 , 0.41839038],[ 0.61295604 , 0.66555018],[ 0.64379346 , 0.92925228],[ 1.1194968  , 0.65876736],[ 0.39495437 , 0.67246734],[ 1.05223282 , 0.17889116],[ 0.97810984 , 1.12794664],[ 0.98392719 , 0.73590255],[ 1.25587405 , 1.21853038],[ 1.01150226 , 1.01835571],[ 1.02251614 , 0.72704228],[ 1.00261519 , 0.95347185],[ 0.96362523 , 0.8607009 ],[ 0.88034659 , 1.2307104 ],[ 0.75907236 , 0.92799796],[ 0.54898709 , 1.69882285],[ 0.55032649 , 0.98831566],[ 1.33360789 , 1.19793298],[ 0.83231239 , 0.8946538 ],[ 1.05173094 , 1.26324289],[ 0.81482231 , 0.56198584],[ 1.03854797 , 1.0553811 ],[ 1.32669227 , 1.61115811],[ 1.13322152 , 1.68151695],[ 0.39754618 , 1.19392967],[ 0.61344185 , 1.05281434],[ 1.18415366 , 0.864884  ]])
    arr2 = np.array([[ 2.15366548 , 1.88035458],[ 2.36978774 , 1.76550283],[ 2.46261387 , 2.10568262],[ 1.90475526 , 1.95242885],[ 1.77712677 , 1.96004856],[ 1.5995514  , 2.1323943 ],[ 1.52727223 , 1.50295551],[ 1.80330407 , 1.57942301],[ 1.86487049 , 1.87234414],[ 1.9586354  , 1.96279729],[ 2.59668134 , 2.414423  ],[ 2.818419   , 1.76280366],[ 2.01511628 , 2.10858546],[ 2.15907962 , 1.81593012],[ 1.63966834 , 2.2209023 ],[ 2.47220599 , 1.70482956],[ 2.08760748 , 2.51601971],[ 1.50547722 , 1.8487145 ],[ 1.68125583 , 2.64968501],[ 2.01924282 , 2.0953572 ],[ 2.22563534 , 2.18266325],[ 2.2684291  , 2.23581599],[ 2.13787557 , 1.9999382 ],[ 1.02638695 , 1.68134967],[ 2.35614619 , 1.32072125],[ 2.20054871 , 1.47401445],[ 1.99454827 , 1.71658741],[ 1.83269065 , 2.47662909],[ 2.40097251 , 2.21823862],[ 2.54404652 , 1.85742018],[ 1.84150027 , 2.06350351],[ 1.69490855 , 1.70169334],[ 1.44745704 , 1.88295233],[ 2.24376639 , 1.67530495],[ 1.42911921 , 1.81854548],[ 1.33789289 , 2.27686128],[ 2.43509821 , 1.95032131],[ 1.9512447  , 1.4595415 ],[ 2.13041192 , 1.79372755],[ 2.2753866  , 2.23781951],[ 2.26753401 , 1.78149305],[ 2.06505449 , 2.01939606],[ 2.44426826 , 2.1437101 ],[ 2.16607141 , 2.31077167],[ 1.96097237 , 2.49100193],[ 1.37255424 , 1.60735016],[ 1.63947758 , 2.17852314],[ 2.13722666 , 2.00559707],[ 1.222696   , 1.67075059],[ 2.56982685 , 2.51218813]])
    x.append(arr1)
    x.append(arr2)
  if SHOW_PIC == 1:
    figure, ax = plt.subplots()
    ax.set_xlim(left=-1, right=4)
    ax.set_ylim(bottom=-1, top=4)
    for i in range(len(arr1)):
      plt.plot(arr1[i][0], arr1[i][1], 'b--', marker='+', color='g')
    for i in range(len(arr2)):
      plt.plot(arr2[i][0], arr2[i][1], 'b--', marker='o', color='b')
    plt.xlabel("x1")
    plt.ylabel("x2")
    plt.plot()
    plt.show()

def calcPhi(x):
  return len(x[1])/(len(x[0])+len(x[1]))

def calcMu(x,i):
  return x[i].mean(axis=0)

def calcSigma(x,mu_0,mu_1):
  sum=np.array([[0,0],[0,0]])
  x0=x[0]
  for i in range(len(x0)):
    z0=np.array([x0[i]-mu_0])
    z0T = np.array([x0[i]-mu_0]).transpose()
    sum = sum + np.dot(z0T, z0)
    print(np.dot(z0T, z0))
  x1=x[1]
  for i in range(len(x1)):
    z1=np.array([x1[i]-mu_1])
    z1T = np.array([x1[i]-mu_1]).transpose()
    sum = sum + np.dot(z1T, z1)
    print(np.dot(z1T, z1))
  return sum/(len(x0)+len(x1))

def classify(x,mu_0,mu_1,sigma,phi):
  var0 = multivariate_normal(mean=mu_0.tolist(), cov=sigma.tolist())
  var1 = multivariate_normal(mean=mu_1.tolist(), cov=sigma.tolist())
  # p(y=1|x) = p(x|y=1)/p(y=1) / p(x) = p(x|y=1)p(y=1) / (p(x|y=1)p(y=1)+p(x|y=0)p(y=0))
  return var1.pdf(x)*phi/(var1.pdf(x)*phi+var0.pdf(x)*(1-phi)) > 0.5

def testClassify(mu_0,mu_1,sigma,phi):
  if SHOW_PIC != 2:
    return
  figure, ax = plt.subplots()
  ax.set_xlim(left=-1, right=4)
  ax.set_ylim(bottom=-1, top=4)
  for i in range(100):
    x1 = random.randint(0,3000)/1000
    x2 = random.randint(0,3000)/1000
    if( classify([x1,x2],mu_0,mu_1,sigma,phi)) == True:
      plt.plot(x1, x2, 'b--', marker='+', color='g')
    else:
      plt.plot(x1, x2, 'b--', marker='o', color='b')
  # draw y = -x+3
  (line1_xs, line1_ys) = [(0, 3), (3, 0)]
  ax.add_line(Line2D(line1_xs, line1_ys, linewidth=1, color='blue'))
  plt.xlabel("x1")
  plt.ylabel("x2")
  plt.plot()
  plt.show()

if __name__ == "__main__":
  # 0 debug option
  MAKE_DATA = False
  SHOW_PIC = 1        # 0 - do not show   1 - show sample data    2 - show test data

  # 1 make the sample
  # the format of x is [ndarray0,ndarray1] , ndarray1 is the set of the first class, we set y=0.
  # ndarray1 is the set of the second class, we set y=1
  x = []
  make_data(x)

  if MAKE_DATA == True:
    exit(0)

  # 2 learn from the sample
  print("hello")
  phi = calcPhi(x)                # phi  = p(y=1)  means close (2,2)
  mu_0 = calcMu(x,0)
  mu_1 = calcMu(x,1)
  sigma = calcSigma(x,mu_0,mu_1)
  print(phi,", ",mu_0,", ",mu_1)
  print(sigma.tolist())

  print("---------")
  # 3 test classify
  testClassify(mu_0,mu_1,sigma,phi)

对于两个协方差相同的样本，我们知道两组数据有相同的概率分布曲线，具体都应该是一个个同心圆。因此，我们可以确定一条垂直于两点连线的曲线是对该样本的理论上正确的分割。因此，我们得到如下结果，并与理论分割的曲线，即\(y=-x+3\)比较，发现对我们随机产生的样本分类效果非常好。

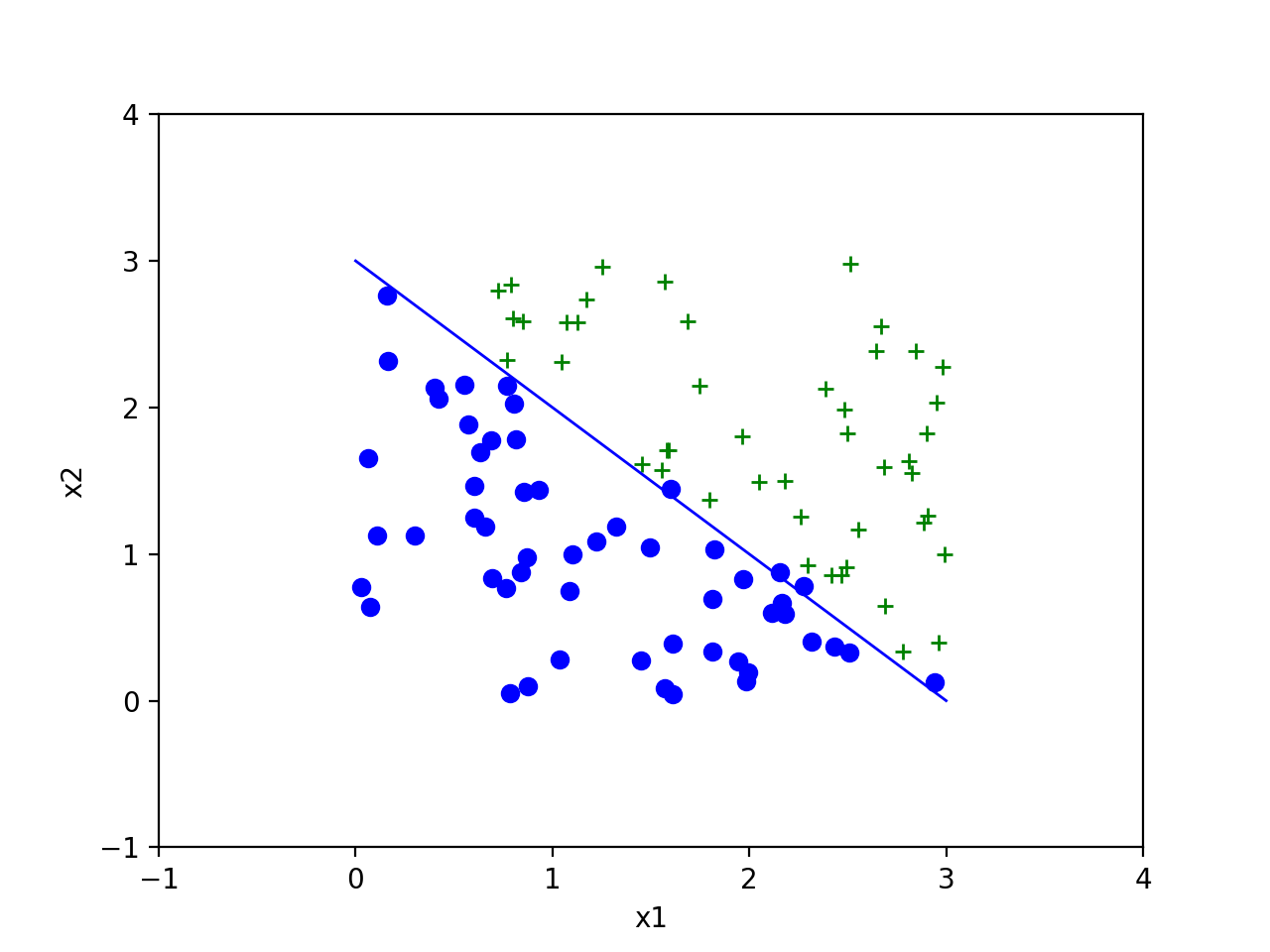
附录 A 相关公式

Hessian矩阵定义:

$${\nabla _A}f(A) = \left( {\begin{array}{*{20}{c}} {\frac{{\partial f}}{{\partial {A _{11}}}}}& \ldots &{\frac{{\partial f}}{{\partial {A _{1n}}}}} \\\ \vdots & \ddots & \vdots \\\ {\frac{{\partial f}}{{\partial {A _{n1}}}}}& \cdots &{\frac{{\partial f}}{{\partial {A _{nn}}}}} \end{array}} \right)$$

矩阵的迹的定义:

$$trA = \sum\limits _{i = 1}^n {{A _{ii}}}$$

关于矩阵迹的公式:

$$tr(a) = a$$ $$tr(aA) = atr(A)$$ $$tr(aA) = atr(A)$$ $$tr(ABC) = tr(CAB) + tr(BCA)$$ $$trA = tr{A^T}$$ $$tr(A + B) = trA + trB$$ $${\nabla _A}tr(AB) = {B^T}$$ $${\nabla _{A^T}}f(A) = {({\nabla _A}f(A))^T}$$ $${\nabla _{A^T}}trAB{A^T}C = CAB + {C^T}A{B^T}$$ $${\nabla _{A^T}}trAB{A^T}C = CAB + {C^T}A{B^T}$$

对矩阵做展开能证明上述大部分公式，这里暂时略。

附录B

手写公式和word版博客地址:

1
https://github.com/zhengchenyu/MyBlog/tree/master/doc/mlearning/生成型学习算法