机器学习-2.7-监督学习之支持向量机

支持向量机(SVM)

1 Margins(间隔)

对于一个逻辑回归问题，\(p(y = 1|x, \theta )\)可以通过下面的式子表示：

$${h _ \theta }(x) = g({\theta ^T}x)$$

\(\theta^Tx\)越大， \(g({\theta ^T}x)\)就越大， 我们就有可高的信心认为\(y=1\)。 同理假如\({ h _\theta }(x) << 0\), 我们就有很强的信息认为\(y=0\)。 (注: >> 表示远大于，<<表示远小于)

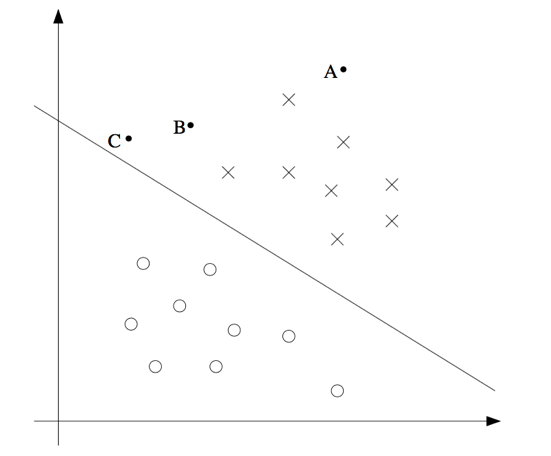
上面这张图，x为正样本，o为负样本。中间的直线是分割超平面。上面图中，我们可以知道对于样本A，我们有很强的信心认为\(y=1\)。然后对于C却接近边界，如果稍微改变分割超平面，就可能导致\(y=0\)。因此，越远离分割超平面的样本，我们越有信息获得他的分类。

2 函数化与几何间隔

区别与之前的逻辑回归。引入支持向量机，我们需要重新定义符号。对于SVM问题, \(y \in \{ - 1,1\} \),定义函数为:

$${h_{w,b}}(x) = g({w^T}x + b)$$

对于\(z = {w^T}x + b > 0\), 有\({h _ \theta }(x) = 1\)。 否则\({h _ \theta }(x) = -1\)。

函数化几何间隔，有如下公式:

$${\hat \gamma ^{(i)}} = {y^{(i)}}({w^T}x + b)$$

上式很容易理解，对于正样本\(y=1\),对于负样本\(y=-1\)。因此可以得到\({\hat \gamma ^{(i)}}\)为一个正值。我们可以就可以定义其为几何间隔，可以理解为距离。根据上一节的分析，一个超平面对样本分割的好坏，取决于距离超平面最近的样本。因为我们定义最小间隔如下：

$$\hat \gamma = {\min _{i = 1,...,m}}{\hat \gamma ^{(i)}}$$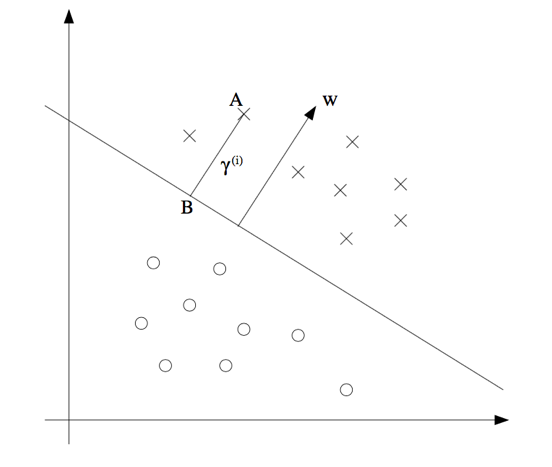

根据上图，我们知道向量\(w\)与超平面\({w^T}x + b = 0\)垂直。

在超平面找任意两点做直线，易证其与法向量內积为零。因此可知法向量与平面垂直。

我们可以得知B点的坐标为\({x^{(i)}} - {r^{(i)}}\frac{w}{||w||}\)，我们将坐标代入超平面方程，有:

$${w^T}({x^{(i)}} - {r^{(i)}}\frac{w}{||w||}) + b = 0$$

由于知道\(||w|| = {w^T}w\)，有：

$${r^{(i)}} = {(\frac{w}{||w||})^T}{x^{(i)}} + \frac{b}{||w||}$$

上面公式对应于正样本，对于负样本则需要加一个符号。因此我们可以综合得到如下公式:

$${r^{(i)}} = {y^{(i)}}({(\frac{w}{||w||})^T}{x^{(i)}} + \frac{b}{||w||})$$

对于公式\({\hat \gamma ^{(i)}} = {y{(i)}}({wT}x + b)\)中，\(||w|| = 1\)的时候为几何间隔。上面的式子实际上就是定义了几何间隔。我们通过定义了向量\(w\)的尺度，这样不会因为选择w比例的不同而产生不同间隔的问题。

3 最优间隔分类器

以下假定我们样本数据是严格线性可分的，否则通过间隔最大化来计算就毫无意义了。

根据前面的分析，我们只需要找到超平面，使得间隔\(\hat \gamma \)最大即可。因此我们可以得到如下最优化问题:

$$\begin{gathered} & {\max _{w,b}}\gamma \hfill \\\ s.t.: & {y^{(i)}}({w^T}{x^{(i)}} + b) \geqslant \gamma , & i = 1,...,m \hfill \\\ & ||w|| = 1 \hfill \\\ \end{gathered} $$

由于\(||w|| - 1 = 0\)不是凸函数，所以需要转化问题。
注> 为什么凸函数如此重要？因为对于一个凸优化问题，认为局部极小值点必为全局极小值点。对\(f(\lambda x + (1 - \lambda )y) \leqslant \lambda f(x) + (1 - \lambda )f(y)\),其中\(0 \leqslant \lambda \leqslant 1\),则\(f(x)\)为凸函数。可以理解为类似于\(y = {x^2}\)的图形。然而对于\(||w|| - 1 = 0\)，具体为\(\sqrt {w _1^2 + w _2^2 + … + w _n^2} = 1\)，二维的情景可以理解为一个圆，三维的话则为一个球。几何图形中，可以发现对于球或圆的上半部分正好与凸函数相反，因此不是凸函数。可以代入公式证明。
进一步转化问题，如下：

$$\begin{gathered} & {\max _{w,b}}\frac{\gamma }{||w||} \hfill \\\ s.t.: & {y^{(i)}}({w^T}{x^{(i)}} + b) \geqslant \gamma , & i = 1,...,m \hfill \\\ \end{gathered} $$

我们知道\(\gamma \)大小，取决于\(w\)和\(b\)的尺度，但是\(w\)和\(b\)的尺度的改变不会影响分配效果。因此我们固定\(\gamma \)为1。将问题转化为:

$$\begin{gathered} & {\min _{w,b}}\frac{1}{2}||w|{|^2} \hfill \\ s.t.: & {y^{(i)}}({w^T}{x^{(i)}} + b) \geqslant 1, & i = 1,...,m \hfill \\ \end{gathered}$$

事实上对于这个问题，我们可以换一种几何意义的解释。如下图所示，我们需要找到\({w^T}x + b = 1\)和\({w^T}x + b = -1\)能够有效分割样本，并且保证是两个超平面之间间隔最大，即使\(\frac{2}{||w||}\)最大，也就意味着使\(\frac{1}{2}||w|{|^2}\)最小。同样我们可以得到上面的优化问题。

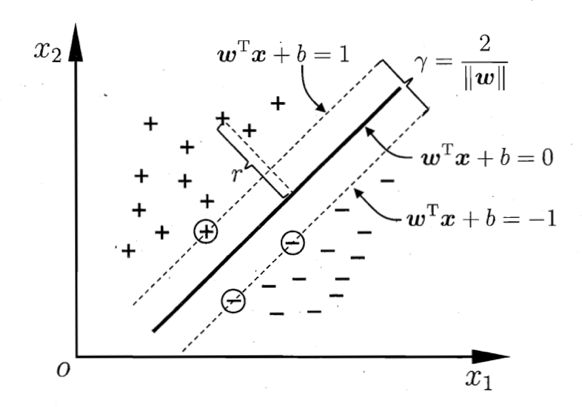
另外，我们距离超平面最近的点，即\(\gamma = 1\)的点，我们称之为支持向量。

4 拉格朗日对偶问题

在对计算上一级得到的优化问题之前，我们介绍一下拉格朗日对偶问题与KKT条件，以便于更容易解决问题。考虑一个通用的优化问题，如下：

$$\begin{gathered} & {\min _x}f(x) \hfill \\\ s.t.: & {g _i}(x) \leqslant 0, & i = 1,...,k \hfill \\\ & {h _j}(x) = 0, & j = 1,...,l \hfill \\\ \end{gathered} $$

然后得到拉格朗日函数，如下：

$$L(x,\alpha ,\beta ) = f(x) + \sum\limits _{i = 1}^k {{\alpha _i}{g _i}(x)} + \sum\limits _{j = 1}^l {{\beta _i}{h _i}(x)} $$ $${\alpha _i} \geqslant 0$$

对于我们的原始问题如何用拉格朗日函数表达呢？我们知道上面的拉格朗日后面两项的最大值为零。因此我们就可以将原始问题转化为以\({\alpha _i}\)和\({\beta _i}\)为参数情况下，求拉格朗日函数的最大值。具体转化为如下形式:

$${\theta _P}(x) = {\max _{\alpha ,\beta ;{\alpha _i} \geqslant 0}}L(x,\alpha ,\beta )$$

然后我们上面的式子，关于x取极小值，就与目标问题一致了。原始为的最优解最终可以通过如下方式表述:

$${p^*} = {\min _x}{\theta _P}(x) = {\min _x}{\max _{\alpha ,\beta ;{\alpha _i} \geqslant 0}}L(x,\alpha ,\beta )$$

我们这里可以写出其对偶问题：

$${\theta _D}(\alpha ,\beta ) = {\min _x}L(x,\alpha ,\beta )$$

对偶问题的最优解如下：

$${d^*} = {\max _{\alpha ,\beta ;{\alpha _i} \geqslant 0}}{\theta _D}(\alpha ,\beta ) = {\max _{\alpha ,\beta ;{\alpha _i} \geqslant 0}}{\min _x}L(x,\alpha ,\beta )$$

我们知道maxmin<minmax,所以我们得到如下式子:

$${d^*} = {\max _{\alpha ,\beta ;{\alpha _i} \geqslant 0}}{\min _x}L(x,\alpha ,\beta ) \leqslant {\min _x}{\max _{\alpha ,\beta ;{\alpha _i} \geqslant 0}}L(x,\alpha ,\beta ) = {p^\*}$$

对于上面的式子只要\(f _i\)和\(g _i\)为凸函数，\(h _i\)为仿射函数，即可使等式两端相等。

仿射函数为线性函数加截距。
另外对于该问题的最优值必满足KKT条件。另外，上述拉格朗日函数对相应参数需要取得极值。最终得到如下条件:

$$\frac{\partial }{{\partial {x _i}}}L({x^*},{\alpha^*},{\beta^*}) = 0$$ $$\frac{\partial }{{\partial \beta }}L({x^*},{\alpha ^*},{\beta ^*}) = 0$$ $${\alpha ^*}{g _i}(x) = 0$$ $${g _i}(x) \leqslant 0$$ $${\alpha ^*} \geqslant 0$$

KKT条件的原理暂时不深入，目前处于应用阶段，有时间再考虑具体原理。

5 最优边界分类器

将我们的优化问题转化为如下标准型：

$$\begin{gathered} & {\min _{w,b}}\frac{1}{2}||w|{|^2} \hfill \\\ s.t.: & - {y^{(i)}}({w^T}{x^{(i)}} + b) + 1 \leqslant 0, & i = 1,...,n \hfill \\\ \end{gathered} $$

根据前面的说明，我们可以通过解对偶问题最优解来获得该问题的最优解。
首先写出拉格朗日对偶函数：

$$L(w,b,\alpha ) = \frac{1}{2}||w|{|^2} - \sum\limits _{i = 1}^m {{\alpha _i}({y^{(i)}}({w^T}{x^{(i)}} + b) - 1)} $$

参数上一节的公式，这里\(w\)和\(b\)对应于\(x\)。我们需要关于\(w\)，\(b\)求极小值，然后求得的极值点代入拉格朗日函数，然后求转化后的拉格朗日函数的极大值即可。

$$\frac{\partial }{{\partial w}}L(w,b,\alpha ) = w - \sum\limits _{i = 1}^m {{\alpha _i}{y^{(i)}}{x^{(i)}}} = 0$$ $$\frac{\partial }{{\partial b}}L(w,b,\alpha ) = \sum\limits _{i = 1}^m {{\alpha _i}{y^{(i)}}} = 0$$

得到\(w = \sum\limits _{i = 1}^m {\alpha _i}{y{(i)}{x{(i)}}} \)，\(\sum\limits _{i = 1}^m {\alpha _i}{y^{(i)}} = 0\)。然后将其代入拉格朗日函数：

$$L(\alpha ) = \frac{1}{2}{w^T}w - \sum\limits _{i = 1}^m {{\alpha _i}({y^{(i)}}({w^T}{x^{(i)}} + b) - 1)} $$ $$L(\alpha ) = - \frac{1}{2}{(\sum\limits _{i = 1}^m {{\alpha _i}{y^{(i)}}{x^{(i)}}} )^T}(\sum\limits _{i = 1}^m {{\alpha _i}{y^{(i)}}{x^{(i)}}} ) + \sum\limits _{i = 1}^m {{\alpha _i}} $$

由于\({\alpha _i}\)和\({y^{(i)}}\)为变量，实际上面的式子就是一个\((Ax + By + Cz)(Ax + By + Cz)\)的问题。因此可以归纳为如下公式：

$$L(\alpha ) = - \frac{1}{2}\sum\limits _{i = 1}^m {\sum\limits _{j = 1}^m {{\alpha _i}{\alpha _j}{y^{(i)}}{y^{(j)}} < {x^{(i)}},{x^{(j)}} > } } + \sum\limits _{i = 1}^m {{\alpha _i}} $$

问题就转化为：

$$\begin{gathered} & {\max _\alpha }L(\alpha ) = - \frac{1}{2}\sum\limits _{i = 1}^m {\sum\limits _{j = 1}^m {{\alpha _i}{\alpha _j}{y^{(i)}}{y^{(j)}} < {x^{(i)}},{x^{(j)}} > } } + \sum\limits _{i = 1}^m {{\alpha _i}} \hfill \\\ s.t.: & {\alpha _i} \geqslant 0 \hfill \\\ & \sum\limits _{i = 1}^n {{\alpha _i}{y^{(i)}}} = 0 \hfill \\\ \end{gathered} $$

由于我们知道支持向量的间隔必须为1，因此我们可以根据其计算\(b\)。设支持向量的集合为S,对属于结合S的样本有\({y{(i)}}({wT}{x^{(i)}} + b) = 1\)。由于\(w = \sum\limits _{i = 1}^m {\alpha _i}{y{(i)}}{x{(i)}} \)，又由于对所有的非支持向量，有\({\alpha _i} = 0\)。因此我们可以综合均值得到：

$$b = \frac{1}{{|S|}}\sum\limits _{i = 1}^S {({y^{(i)}} - \sum\limits _{j = 1}^S {{\alpha _j}{y^{(j)}} < {x^{(i)}},{x^{(j)}} > } )} $$

6 正则化

关于之前的问题我们假定样本严格可分。但是实际上需要容忍一些误差。因此我们将公式修正为如下形式(C为常数)：

$$\begin{gathered} & {\min _{w,b,\xi }}\frac{1}{2}||w|{|^2} + C\sum\limits _{i = 1}^m {{\xi _i}} \hfill \\\ s.t.: & {y^{(i)}}({w^T}{x^{(i)}} + b) \geqslant 1 - {\xi _i} & & i = 1,...,m \hfill \\\ & {\xi _i} \geqslant 0 & & & & i = 1,...,m \hfill \\\ \end{gathered} $$

我们允许\({y{(i)}}({wT}{x^{(i)}} + b)\)小于1，但是不希望小太多。所以，我们需要保证\({\xi _i}\)的总和尽可能小，因此得上面的式子。然后我们可以得到拉格朗日公式如下：

$$L(w,b,\xi ,\alpha ,r) = \frac{1}{2}||w|{|^2} + C\sum\limits _{i = 1}^m {{\xi _i}} - \sum\limits _{i = 1}^m {{\alpha _i}({y^{(i)}}({w^T}{x^{(i)}} + b) - 1 + {\xi _i})} - \sum\limits _{i = 1}^m {{r _i}{\xi _i}} $$

对\(w\)，\(b\)，\(\xi \), 求导得:

$$\frac{\partial }{{\partial w}}L(w,b,\xi ,\alpha ,r) = w - \sum\limits _{i = 1}^m {{\alpha _i}{y^{(i)}}{x^{(i)}}} = 0$$ $$\frac{\partial }{{\partial b}}L(w,b,\xi ,\alpha ,r) = - \sum\limits _{i = 1}^m {{\alpha _i}{y^{(i)}}} = 0$$ $$\frac{\partial }{{\partial {\xi _i}}}L(w,b,\xi ,\alpha ,r) = C - {r _i} - {\alpha _i} = 0$$

可以得到\(w = \sum\limits _{i = 1}^m {\alpha _i}{y{(i)}}{x{(i)}}\),\(\sum\limits _{i = 1}^m {\alpha _i}{y^{(i)}} = 0\),\(C = {r _i} + {\alpha _i}\)。其中我们知道\({r _i} \geqslant 0\)，所以也可得到\(0 \leqslant {\alpha _i} \leqslant C\)。带入拉格朗日函数得:

$$L(\alpha ) = - \frac{1}{2}\sum\limits _{i = 1}^m {\sum\limits _{j = 1}^m {{\alpha _i}{\alpha _j}{y^{(i)}}{y^{(j)}} < {x^{(i)}},{x^{(j)}} > } } + \sum\limits _{i = 1}^m {({r _i} + {\alpha _i}){\xi _i}} - \sum\limits _{i = 1}^m {{\alpha _i}({\xi _i}} - 1) - \sum\limits _{i = 1}^m {{r _i}{\xi _i}} $$

我们对上面的式子乘以-1，转化为求最小值的问题，可以得到最终的优化问题：

$$\begin{gathered} & \min L(\alpha ) = \min \frac{1}{2}\sum\limits _{i = 1}^m {\sum\limits _{j = 1}^m {{\alpha _i}{\alpha _j}{y^{(i)}}{y^{(j)}} < {x^{(i)}},{x^{(j)}} > } } - \sum\limits _{i = 1}^m {{\alpha _i}} \hfill \\\ s.t.: & \sum\limits _{i = 1}^m {{\alpha _i}{y^{(i)}}} = 0 \hfill \\\ & 0 \leqslant {\alpha _i} \leqslant C \hfill \\\ \end{gathered} $$

可以得到如下的KKT条件：

$${\alpha _i},{r _i} \geqslant 0$$ $${y^{(i)}}({w^T}{x^{(i)}} + b) - 1 + {\xi _i} \geqslant 0$$ $${\alpha _i}({y^{(i)}}({w^T}{x^{(i)}} + b) - 1 + {\xi _i}) = 0$$ $${\xi _i} \geqslant 0,{r _i}{\xi _i} = 0$$

对于上述KKT条件我们可以转换为如下形式：

$${y^{(i)}}({w^T}{x^{(i)}} + b) \geqslant 1 , {\alpha _i} = 0$$ $${y^{(i)}}({w^T}{x^{(i)}} + b) \leqslant 1 , {\alpha _i} = C$$ $${y^{(i)}}({w^T}{x^{(i)}} + b) = 1 , 0 \leqslant {\alpha _i} \leqslant C$$

很容易转化上面的式子，三个条件分别表示在比支持向量距离分割超平面远的样本，比支持向量距离分割超平面近的可容忍的误差样本，支持向量对应的样本。

7 SMO算法理论

这一节使用SMO算法解决上一节归纳出来的优化问题。
SMO算法的思想来自于坐标上升算法，坐标上升算法的主要思想是一次遍历一个变量，然后把其他变量当做是常亮，进在一个维度上优化。
然后对于我们之前的问题，有\(\sum\limits _{i = 1}^m {\alpha _i}{y^{(i)}} = 0\)。设置我们设\(\zeta = {\alpha _1}{y^{(1)}} + {\alpha _2}{y^{(2)}} = \sum\limits _{i = 3}^m {\alpha _i}{y^{(i)}} \)，将\({\alpha _1}\)用\({\alpha _2}\)表达，然后得到关于\({\alpha _2}\)的二次函数，这样很容易取得极值。当所有样本满足KKT条件，且无法继续增加，我们就可以认为此刻取得最优值。

由于我们知道\(0 \leqslant {\alpha _i} \leqslant C\)，所以我们可以求的其取值范围，我们可以将二维变量表述为一个方格内，具体如下：

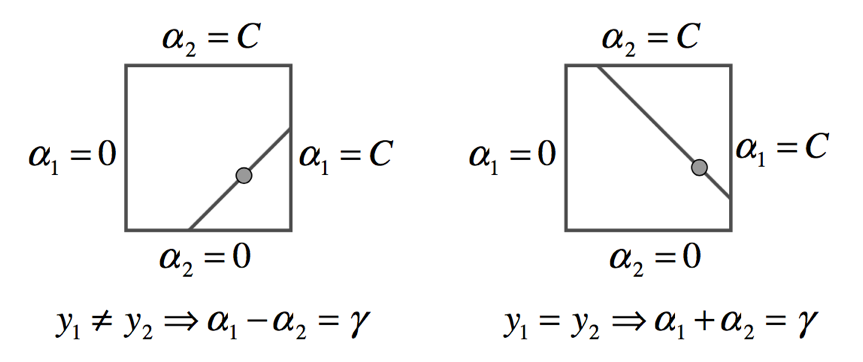
最多四种情况代入，经过求截距等一系列操作，可以将的取值范围归纳为下面的公式，其中L表示上界，H表示上界。
同号时有：

$$L = \max (0,\alpha _1^{old} + \alpha _2^{old} - C)$$ $$H = \min (C,\alpha _1^{old} + \alpha _2^{old})$$

异号的时候有：

$$L = \max (0,\alpha _2^{old} - \alpha _2^{old})$$ $$H = \min (C,C + \alpha _2^{old} - \alpha _1^{old})$$

进一步求解二次规划问题：

$$\psi ({\alpha _1},{\alpha _2}) = \frac{1}{2}\alpha _1^2k(1,1) + \frac{1}{2}\alpha _2^2k(2,2) + {y^{(1)}}{y^{(2)}}{\alpha _1}{\alpha _2}k(1,2) - {\alpha _1} - {\alpha _2} + {y^{(1)}}{\alpha _1}{v _1} + {y^{(2)}}{\alpha _2}{v _2} + M$$

上式中\(k(i,j) = < {x _i},{x _j} > \)具体是核函数的简写，下节会介绍。\(M\)为与\(\alpha _1\),\(\alpha _2\)无关的参数。另外，\({v _1} = \sum\limits _{i = 3}^m {\alpha _i}{y^{(i)}}k(1,i) \),\({v _2} = \sum\limits _{i = 3}^m {\alpha _i}{y^{(i)}}k(2,i) \)。

我们设\(\zeta = {\alpha _1}{y^{(1)}} + {\alpha _2}{y^{(2)}}\)，所以有\({\alpha _1} = {y^{(1)}}(\zeta - {\alpha _2}{y^{(2)}})\),代入上式:

$$\psi ({\alpha _2}) = \frac{1}{2}{(\zeta - {\alpha _2}{y^{(2)}})^2}k(1,1) + \frac{1}{2}\alpha _2^2k(2,2) + {y^{(2)}}(\zeta - {\alpha _2}{y^{(2)}}){\alpha _2}k(1,2) - (\zeta - {\alpha _2}{y^{(2)}}){y^{(1)}} - {\alpha _2} + (\zeta - {\alpha _2}{y^{(2)}}){v _1} + {y^{(2)}}{\alpha _2}{v _2} + M$$

然后求导数:

$$\frac{\partial }{{\partial {\alpha _2}}}\psi ({\alpha _2}) = ({\alpha _2}{y^{(2)}} - \zeta ){y^{(2)}}k(1,1) + {\alpha _2}k(2,2) + {y^{(2)}}\zeta k(1,2) - 2{\alpha _2}k(1,2) + {y^{(1)}}{y^{(2)}} - {y^{(1)}}{y^{(2)}} - {y^{(2)}}{v _1} + {y^{(2)}}{v _2} = 0$$ $$\frac{\partial }{{\partial {\alpha _2}}}\psi ({\alpha _2}) = {\alpha _2}(k(1,1) + k(1,2) - 2k(1,2)) - \zeta {y^{(2)}}k(1,1) + \zeta {y^{(2)}}k(1,2) + {y^{(1)}}{y^{(2)}} - {y^{(1)}}{y^{(2)}} - {y^{(1)}}{v _1} + {y^{(2)}}{v _2} = 0$$

我们设\(\eta = k(1,1) + k(1,2) - 2k(1,2)\)，对\(\eta\)大于0的情况，导数为0的极值点就是极小值。对于\(\eta\)小于等于0的情况，最小值点肯定取自于边界，我们需要比较函数在\(L\)和\(H\)的大小。

让我们继续简化上面的式子，对于\(\eta\)大于0的情况下，取得极值。由于我们轻易得到下面的关系。

$${v_1} = \sum\limits _{i = 1}^m {{\alpha _i}{y^{(2)}}k(1,i)} + b - b - \sum\limits _{i = 1}^2 {{\alpha _i}{y^{(2)}}k(1,i)} = f({x^{(1)}}) - b - \sum\limits _{i = 1}^2 {{\alpha _i}{y^{(2)}}k(1,i)} $$ $${v_2} = \sum\limits _{i = 1}^m {{\alpha _i}{y^{(2)}}k(2,i)} + b - b - \sum\limits _{i = 1}^2 {{\alpha _i}{y^{(2)}}k(2,i)} = f({x^{(2)}}) - b - \sum\limits _{i = 1}^2 {{\alpha _i}{y^{(2)}}k(2,i)} $$

将上面的关系代入的如下极值：

$$\alpha _2^{new} = \frac{{\zeta {y^{(2)}}k(1,1) - \zeta {y^{(2)}}k(1,2) + {y^{(2)}}({y^{(1)}} - f({x^{(1)}}) - ({y^{(2)}} - f({x^{(2)}})) - {y^{(2)}}\sum\limits _{i = 1}^2 {\alpha _i^{old}{y^{(2)}}k(1,i)} + {y^{(2)}}\sum\limits _{i = 1}^2 {\alpha _i^{old}{y^{(2)}}k(2,i)} }}{\eta }$$

我们将\(\zeta = {\alpha _1}{y^{(1)}} + {\alpha _2}{y^{(2)}}\)代入上式，得:

$$\alpha _2^{new} = \frac{{{\alpha _1}{y^{(1)}}{y^{(2)}}k(1,1) + {\alpha _2}k(1,1) - {\alpha _1}{y^{(1)}}{y^{(2)}}k(1,2) - {\alpha _2}k(1,2) - {\alpha _1}{y^{(1)}}{y^{(2)}}k(1,1) - {\alpha _2}k(1,2) + {\alpha _2}{y^{(1)}}{y^{(2)}}k(1,2) + {\alpha _2}k(2,2) + {y^{(2)}}({y^{(1)}} - f({x^{(1)}}) - ({y^{(2)}} - f({x^{(2)}}))}}{\eta }$$

约掉部分选项，有:

$$\alpha _2^{new} = \alpha _2^{old} + \frac{{{y^{(2)}}({y^{(1)}} - f({x^{(1)}}) - ({y^{(2)}} - f({x^{(2)}})))}}{\eta }$$ $$\alpha _2^{new} = \alpha _2^{old} + \frac{{{y^{(2)}}({e _1} - {e _2})}}{\eta }$$

接下来就只剩下求\(b\)的问题了，根据上一节最后转化的KKT条件。对\(0 \leqslant {\alpha _1} \leqslant C\)的情况下，有\({y{(1)}}({wT}{x^{(1)}} + b) = 1\)。所以有：

$$b = {y^{(1)}} - \sum\limits _{i = 1}^m {{\alpha _i}} {y^{(i)}}k(1,i)$$

进一步展开有：

$$b = {y^{(1)}} - \sum\limits _{i = 3}^m {\alpha _i^{new}{y^{(i)}}k(1,i)} - \alpha _1^{new}{y^{(1)}}k(1,1) - \alpha _2^{new}{y^{(2)}}k(1,2)$$

我们知道上面的式子中\({\alpha _3}\)到\({\alpha _m}\)并没有发生变化，因此有：

$$\sum\limits _{i = 3}^m {\alpha _i^{new}{y^{(i)}}k(1,i)} = \sum\limits _{i = 3}^m {\alpha _i^{old}{y^{(i)}}k(1,i)} = \sum\limits _{i = 1}^m {\alpha _i^{old}{y^{(i)}}k(1,i)} - \alpha _1^{old}{y^{(1)}}k(1,1) - \alpha _2^{old}{y^{(2)}}k(1,2) = f({x^{(1)}}) - b - \alpha _1^{old}{y^{(1)}}k(1,1) - \alpha _2^{old}{y^{(2)}}k(1,2)$$

代入如上式得:

$${b^{new}} = - {e_1} + (\alpha _1^{old} - \alpha _1^{new}){y^{(1)}}k(1,1) + (\alpha _1^{old} - \alpha _1^{new}){y^{(2)}}k(1,2) + {b^{old}}$$

对于\({\alpha _2}\)有同样的道理。

综上，假如\(0 \leqslant {\alpha _1} \leqslant C\)，有:

$${b^{new}} = - {e_1} + (\alpha _1^{old} - \alpha _1^{new}){y^{(1)}}k(1,1) + (\alpha _1^{old} - \alpha _1^{new}){y^{(2)}}k(1,2) + {b^{old}}$$

假如\(0 \leqslant {\alpha _2} \leqslant C\)，有：

$${b^{new}} = - {e_2} + (\alpha _2^{old} - \alpha _2^{new}){y^{(1)}}k(2,1) + (\alpha _2^{old} - \alpha _2^{new}){y^{(2)}}k(2,2) + {b^{old}}$$

假如\(0 \leqslant {\alpha _1},{\alpha _2} \leqslant C\),事实上上面两个公司的出来的结果是一样的，因此不用特殊计算。
如果不满足在\(0\)和\(C\)的范围，则去两个公式的中间值。(笔者认为没有必要更新)

8 SMO算法实践

在SMO论文中有具体的伪代码，算法的主要逻辑就是要保证每个样本都满足KKT条件，且直到所有\(\alpha \)达到极值，即不需要更新为止。

然后是关于\(\alpha \)的选择，第一个\(\alpha \)我们可以随机选择一个违反KKT条件的，第二个我们选择能够最大程度更新\(\alpha \)的值，看上一节的公式，实际会选择\(|e _1-e _2|\)最大的样本点作为第二个\(\alpha \)。具体逻辑可以参考SMO的论文，或者下面代码的注释。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
import numpy as np
import random
from matplotlib import pyplot as plt
from matplotlib.lines import Line2D

global g_y_vec    # g_y_vec为样本输出, 大小g_m
global g_x_mat    # g_x_mat为样本的输入, 大小2*g_m
global g_m        # g_m 为样本数目
global g_alpha    # g_alpha 大小为g_m
global g_C
global g_w        # 实际没有使用，而是通过alpha表示的
global g_b        # y = wx+b
global g_y_now    # 表示当前参数计算的y，即svmOutPut对应的g_y_now
global g_err      # g_err 表示svmOutput - g_y_vec对应的序列

# g_arr0 means classify of -1
g_arr0 = np.array([[ 0.88235916 , 1.01511634],[ 0.75243817 , 0.76520033],[ 0.95710848 , 1.41894337],[ 1.48682891 , 0.78885043],[ 1.24047011 , 0.71984948],[ 0.67611276 , 1.07909452],[ 1.03243669 , 1.08929695],[ 1.0296548  , 1.25023769],[ 1.54134008 , 0.39564824],[ 0.34645057 , 1.61499636],[ 0.77206174 , 1.23613698],[ 0.91446988 , 1.38537765],[ 0.99982962 , 1.34448471],[ 0.78745962 , 0.9046565 ],[ 0.74946602 , 1.07424473],[ 1.09294839 , 1.14711993],[ 0.39266844 , 0.78788004],[ 0.83112357 , 1.2762774 ],[ 1.05056188 , 1.13351562],[ 1.62101523 , 1.15035562],[ 0.70377517 , 1.1136416 ],[ 1.03715472 , 0.47905693],[ 0.94598381 , 0.8874837 ],[ 0.94447128 , 2.02796925],[ 0.72442242 , 1.09835206],[ 0.69046731 , 1.46232182],[ 1.20744606 , 1.10280041],[ 0.70665746 , 0.82139503],[ 1.08803887 , 1.4450361 ],[ 0.88530961 , 0.75727475],[ 0.98418545 , 0.80248161],[ 0.74970386 , 1.13205709],[ 0.72586454 , 1.06058385],[ 0.9071812  , 1.09975063],[ 0.75182835 , 0.93570147],[ 0.80052289 , 1.08168507],[ 0.40180652 , 0.9526211 ],[ 0.62312617 , 0.84385058],[ 0.68212516 , 1.25912717],[ 1.19773245 , 0.16399654],[ 0.96093132 , 0.43932091],[ 1.25471657 , 0.92371829],[ 1.12330272 , 1.26968747],[ 1.30361985 , 0.99862123],[ 1.23477665 , 1.1742804 ],[ 0.28471876 , 0.5806044 ],[ 1.89355099 , 1.19928671],[ 1.09081369 , 1.28467312],[ 1.40488635 , 0.90034427],[ 1.11672364 , 1.49070515],[ 1.35385212 , 1.35767891],[ 0.92746374 , 1.79096697],[ 1.89142562 , 0.98228303],[ 1.0555218  , 0.86070833],[ 0.69001255 , 1.12874741],[ 0.98137315 , 1.3398852 ],[ 1.02525371 , 0.77572865],[ 1.1354295  , 1.07098552],[ 1.50829164 , 1.43065998],[ 1.09928764 , 1.55540292],[ 0.64695084 , 0.79920395],[ 0.82059034 , 0.97533491],[ 0.56345455 , 1.08168272],[ 1.06673215 , 1.19448556],[ 0.96512548 , 1.5268577 ],[ 0.96914451 , 1.00902985],[ 0.72879413 , 0.92476415],[ 1.0931483  , 1.13572242],[ 1.34765121 , 0.83841006],[ 1.57813788 , 0.65915892],[ 0.59032608 , 0.82747946],[ 0.83838504 , 0.67588473],[ 1.35101322 , 1.21027851],[ 0.71762153 , 0.41839038],[ 0.61295604 , 0.66555018],[ 0.64379346 , 0.92925228],[ 1.1194968  , 0.65876736],[ 0.39495437 , 0.67246734],[ 1.05223282 , 0.17889116],[ 0.97810984 , 1.12794664],[ 0.98392719 , 0.73590255],[ 1.25587405 , 1.21853038],[ 1.01150226 , 1.01835571],[ 1.02251614 , 0.72704228],[ 1.00261519 , 0.95347185],[ 0.96362523 , 0.8607009 ],[ 0.88034659 , 1.2307104 ],[ 0.75907236 , 0.92799796],[ 0.54898709 , 1.69882285],[ 0.55032649 , 0.98831566],[ 1.33360789 , 1.19793298],[ 0.83231239 , 0.8946538 ],[ 1.05173094 , 1.26324289],[ 0.81482231 , 0.56198584],[ 1.03854797 , 1.0553811 ],[ 1.32669227 , 1.61115811],[ 1.13322152 , 1.68151695],[ 0.39754618 , 1.19392967],[ 0.61344185 , 1.05281434],[ 1.18415366 , 0.864884  ]])
# g_arr1 means classify of +1
g_arr1 = np.array([[ 2.15366548 , 1.88035458],[ 2.36978774 , 1.76550283],[ 2.46261387 , 2.10568262],[ 1.90475526 , 1.95242885],[ 1.77712677 , 1.96004856],[ 1.5995514  , 2.1323943 ],[ 1.52727223 , 1.50295551],[ 1.80330407 , 1.57942301],[ 1.86487049 , 1.87234414],[ 1.9586354  , 1.96279729],[ 2.59668134 , 2.414423  ],[ 2.818419   , 1.76280366],[ 2.01511628 , 2.10858546],[ 2.15907962 , 1.81593012],[ 1.63966834 , 2.2209023 ],[ 2.47220599 , 1.70482956],[ 2.08760748 , 2.51601971],[ 1.50547722 , 1.8487145 ],[ 1.68125583 , 2.64968501],[ 2.01924282 , 2.0953572 ],[ 2.22563534 , 2.18266325],[ 2.2684291  , 2.23581599],[ 2.13787557 , 1.9999382 ],[ 1.02638695 , 1.68134967],[ 2.35614619 , 1.32072125],[ 2.20054871 , 1.47401445],[ 1.99454827 , 1.71658741],[ 1.83269065 , 2.47662909],[ 2.40097251 , 2.21823862],[ 2.54404652 , 1.85742018],[ 1.84150027 , 2.06350351],[ 1.69490855 , 1.70169334],[ 1.44745704 , 1.88295233],[ 2.24376639 , 1.67530495],[ 1.42911921 , 1.81854548],[ 1.33789289 , 2.27686128],[ 2.43509821 , 1.95032131],[ 1.9512447  , 1.4595415 ],[ 2.13041192 , 1.79372755],[ 2.2753866  , 2.23781951],[ 2.26753401 , 1.78149305],[ 2.06505449 , 2.01939606],[ 2.44426826 , 2.1437101 ],[ 2.16607141 , 2.31077167],[ 1.96097237 , 2.49100193],[ 1.37255424 , 1.60735016],[ 1.63947758 , 2.17852314],[ 2.13722666 , 2.00559707],[ 1.222696   , 1.67075059],[ 2.56982685 , 2.51218813]])

def calcLH(id1,id2):
  if g_y_vec[id1] == g_y_vec[id2]:
    L = max(0,g_alpha[id1]+g_alpha[id2]-g_C)
    H = min(g_C,g_alpha[id1]+g_alpha[id2])
  else:
    L = max(0,g_alpha[id2]-g_alpha[id1])
    H = min(g_C,g_C+g_alpha[id2]-g_alpha[id1])
  return (L,H)

def svmOutput(id1):
  # 这个函数是svm的实际输出，计算当前参数(w,b)下, 计算得到的y
  # 由于w = sum (alpha*y*x), 对于第i个分量x_i所以输出结果应该为w*x_i+b, 也就是 sum (alpha*y*<x_1-m,x_i>)
  # 注: 待会分析下alpha的变化趋势与C的关系
  global g_b
  sum = 0;
  for i in range(g_m):
    sum += g_alpha[i]*g_y_vec[i]*kernel(i,id1)
  return sum+g_b

def kernel(id1,id2):
  # 这里核函数为简单的内积
  # id1和id2为int类型，是g_x_mat中的索引
  return np.dot(g_x_mat[id1],g_x_mat[id2])

def compareFun(id1,id2,L,H):
  # 如果返回1，表示L处去极小值。如果返回-1，H处去极小值。如果是0，表示这次不更新
  # 如果两者相等，这里略过, 说明无法有强力证据证明这个样本属于wx+b>1还是wx+b<1，所以等待下一轮迭代。因此，与L和H相等应该设置一个阀值，判断近似相等。
  global g_b
  y_1 = g_y_vec[id1]
  y_2 = g_y_vec[id2]
  e_1 = g_err[id1]
  e_2 = g_err[id2]
  alpha_1 = g_alpha[id1]
  alpha_2 = g_alpha[id2]
  k11 = kernel(id1,id1)
  k12 = kernel(id1,id2)
  k22 = kernel(id2,id2)
  s = y_1*y_2
  f_1 = y_1*(e_1+g_b)-alpha_1*k11-s*alpha_2*k12
  f_2 = y_2*(e_2+g_b)-s*alpha_1*k12-alpha_2*k22
  L_1 = alpha_1+s*(alpha_2-L)
  H_1 = alpha_1+s*(alpha_2-H)
  phi_l = L_1*f_1+L*f_2+0.5*L_1*L_1*k11+0.5*L*L*k22+s*L*L_1*k12
  phi_h = H_1*f_1+H*f_2+0.5*H_1*H_1*k11+0.5*H*H*k22+s*H*H_1*k12
  if L==H:
    return 0
  if phi_l < phi_h:
    return 1
  else:
    return -1

def takeStep(id1,id2,err):
  if id1==id2:
    return 0
  alpha_1 = g_alpha[id1]
  alpha_2 = g_alpha[id2]
  y_1 = g_y_vec[id1]
  y_2 = g_y_vec[id2]
  e1 = g_err[id1]
  e2 = g_err[id2]
  s = y_1*y_2
  L,H=calcLH(id1,id2)
  #print("id1=",id1,", id2=",id2," L=",L,", H=",H)
  if L==H :
    return 0
  k11 = kernel(id1,id1)
  k12 = kernel(id1,id2)
  k22 = kernel(id2,id2)
  eta = k11+k22-2*k12
  #print("kernel:",k11,k12,k22,", eta=",eta,"e1=",e1,"e2=",e2)

  alpha_2_new = alpha_2
  # 如果eta大于0, 我们可知最小值在边界或极小值点上。事实上，如果极小值不在范围内，必在距离极小值近的那个边界上。
  # 如果eta小于0, 我们可知最小值则必在边界上。我们只需要比较两个边界点函数的大小即可。
  if eta>0 :
    alpha_2_new = alpha_2+y_2*(e1-e2)/eta
    alpha_2_new = max(alpha_2_new,L)
    alpha_2_new = min(alpha_2_new,H)
  else:
    # 由于我们知道可以直接这是一个关于alpha的二次函数，并且自变量的取值范围是[L,H], 事实上我们只需要比较alpha_2_new离L和H哪个远即可
    # 但是考虑到eta=0的一次函数特殊情况，我们还是老老实实的计算函数值吧。
    ret = compareFun(id1, id2, L, H)
    if ret == 0:
      alpha_2_new = alpha_2
    elif ret == 1:
      alpha_2_new = L
    elif ret == 1:
      alpha_2_new = H
    print("----------------eta<=0----------------")

  # 归整化alpha_2_new
  if alpha_2_new < err:
    alpha_2_new = 0
  elif alpha_2_new > g_C - err:
    alpha_2_new = g_C
  if abs(alpha_2_new-alpha_2) < err:
    print("alpha_2 is no need to update")
    return 0

  # update b
  global g_b
  alpha_1_new = alpha_1 + s * (alpha_2 - alpha_2_new)      # 不必担心alpha_1_new不在[0,C]范围内，之前的公式已经保证了
  b1_new = -e1-y_1*k11*(alpha_1_new-alpha_1)-y_2*k12*(alpha_2_new-alpha_2) + g_b
  b2_new = -e2-y_1*k12*(alpha_1_new-alpha_1)-y_2*k22*(alpha_2_new-alpha_2) + g_b
  if alpha_1_new>0 and not alpha_1_new<g_C:
    g_b = b1_new
  elif alpha_2_new>0 and not alpha_2_new<g_C:
    g_b = b2_new
  else:
    g_b = 0.5*(b1_new+b2_new)

  # update alpha
  g_alpha[id1] = alpha_1_new
  g_alpha[id2] = alpha_2_new
  print("g_alpha[id1]=",g_alpha[id1],"g_alpha[id2]=",g_alpha[id2],"s=",s,", alpha_1=",alpha_1,", alpha_2=",alpha_2)

  # update err g_y_now
  updateYAndErr()

  return 1

def updateYAndErr():
  for i in range(g_m):
    g_y_now[i] = svmOutput(i)
    g_err[i] = svmOutput(i)-g_y_vec[i]

def chooseBestAlphaIndex(id2):
  maxIncr = 0
  maxIndex = -1;
  for i in range(g_m):
    incr = abs(g_err[i]-g_alpha[i])
    if incr >= maxIncr:
      maxIndex = i
      maxIncr = incr
  return maxIndex

def sizeOfNonZerorAndNonC():
  size=0
  for i in range(g_m):
    if g_alpha[i]!=0 and g_alpha[i]!=g_C:
      size= size+1
  return size

def chooseRandomIndex(id2):
  ret = id2;
  while ret==id2:
    ret = random.randint(0,g_m-1)
  return ret

# 对于examineExample函数,我们一次进选择id2样本对应的alpha与如下规则选择的id1对应的alpha,然后相应跟新其值。
def examineExample(id2):
  y_2 = g_y_vec[id2]
  tol = 1e-2        # 是一个正数
  alpha_2 = g_alpha[id2]
  e_2 = svmOutput(id2)-g_y_vec[id2]
  r_2 = e_2 * y_2

  # 我们只对当前违反kkt条件的样本对应的alpha进行更新
  # 关于违反kkt条件的说明:
  # (1) r_2 < -tol 表示r_2小于0，即表示输出的预测结果与样本的y符号相反，因此应该属于误差案例的。所以，根据公式，alpha = C。如果alpha < C ,比违反kkt条件
  # (2) r_2 < -tol 表示r_2大于0，即表示输出的预测结果与样本的y符号相同，当误差大于一定的
  if r_2 < -tol and alpha_2 < g_C or r_2 > tol and alpha_2 > 0 :
    # 下面的程序逻辑是这样的:
    # 先遍历alpha非0或非C, 因为我们对于alpha为0和alpha为C的情况, 认为是处于非支持向量和处于误差样本的情况。我们只有根据支持向量下，找到最优的||w||才有意义
    # 首先，我们找到|e1-e2|最大的alpha, 从这里优化。如果优化结果不理想，我们就随机找一个alpha一起计算。如果还不行，就在整个范围alpha范围内计算
    if sizeOfNonZerorAndNonC()>0:
      id1=chooseBestAlphaIndex(id2)
      if takeStep(id1,id2,1e-3):
        #print("takeStep1, alpha[",id1,"]=",g_alpha[id1],", alphapp[",id2,"]=",g_alpha[id2])
        return 1
    r=chooseRandomIndex(id2)
    for i in range(g_m):
      id1 = (r+i)%g_m
      if id1!=id2 and g_alpha[id1]!=0 and g_alpha[id1]!=g_C:
        if takeStep(id1,id2,1e-3):
          #print("takeStep2, alpha[", id1, "]=", g_alpha[id1], ", alphapp[", id2, "]=", g_alpha[id2])
          return 1
    r = chooseRandomIndex(id2)
    for i in range(g_m):
      id1 = (r + i) % g_m
      if id1 != id2:
        if takeStep(id1,id2,1e-3):
          #print("takeStep3, alpha[", id1, "]=", g_alpha[id1], ", alphapp[", id2, "]=", g_alpha[id2])
          return 1
  return 0

def showPic(w,b):
  # draw wx+b, x1为横轴，x2为纵轴
  k = -w[0]/w[1]
  b = -g_b/w[1]

  figure, ax = plt.subplots()
  ax.set_xlim(left=-1, right=4)
  ax.set_ylim(bottom=-1, top=4)
  for i in range(g_m):
    x = g_x_mat[i]
    if abs(g_alpha[i]-0)<1e-3:
      plt.plot(x[0], x[1], 'b--', marker='+', color='r')
    elif abs(g_alpha[i]-g_C)<1e-3:
      plt.plot(x[0], x[1], 'b--', marker='o', color='g')
    else:
      plt.plot(x[0], x[1], 'b--', marker='o', color='b')
  # draw y = -x+3
  (line1_xs, line1_ys) = [(0, 3), (b, 3*k+b)]
  ax.add_line(Line2D(line1_xs, line1_ys, linewidth=1, color='blue'))
  plt.xlabel("x1")
  plt.ylabel("x2")
  plt.plot()
  plt.show()

if __name__=="__main__":
  # 0 make data
  g_y_vec = np.array([])
  for i in range(len(g_arr0)):
    g_y_vec=np.append(g_y_vec,-1)
  for j in range(len(g_arr1)):
    g_y_vec=np.append(g_y_vec,+1)
  g_x_mat = np.vstack((g_arr0,g_arr1))

  # 1 training
  g_m = len(g_x_mat)
  g_alpha = np.zeros(g_m)
  g_y_now = np.zeros(g_m)
  g_err = np.zeros(g_m)
  global g_b
  g_b = 0
  numChanged = 0
  examineAll = 1
  g_C = 10
  err = 0

  updateYAndErr()       # 实现更新下缓冲，即当前输出与误差值

  while numChanged>0 or examineAll:
    numChanged = 0
    # 循环处理，第一次对所有的样本进行一次处理。
    # 然后对所有非边界的数值进行处理。因为在当前参数下，非边界的样本，我们认为其是支持向量。对于优化||w||的大小，支持向量才有意义。
    if examineAll:
      for i in range(g_m):
        numChanged += examineExample(i)
        #print("examineAll=1, numChanged=",numChanged)
    else:
      for i in range(g_m):
        if g_alpha[i]!=0 and g_alpha[i]!=g_C:
          numChanged += examineExample(i)
    examineAll = abs(examineAll-1)
  #print(g_alpha)

  # 3 show
  # 计算w
  w = np.array([0,0])
  for i in range(g_m):
    if g_alpha[i]!=0:
      w=np.add(w,g_y_vec[i]*g_alpha[i]*g_x_mat[i])

  showPic(w,g_b)
  #print(g_alpha)

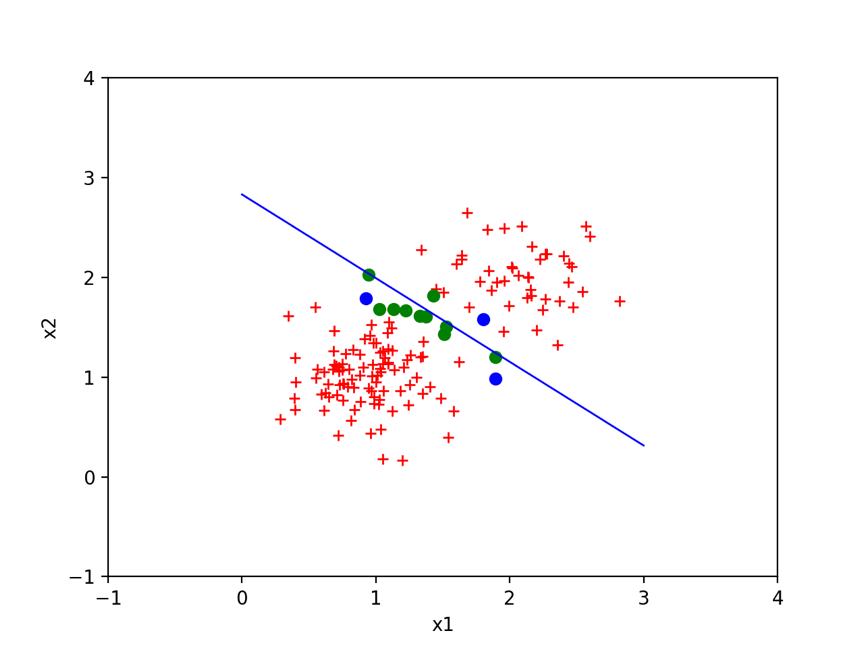
经过数轮迭代得到如下结果，其中直线为得到的分割曲线，蓝色点为支持向量，红色点是那些有良好分类的样本，绿色点为可容忍的误差样本。

9 核函数

SMO另个非常强大的地方上，它能够很好的解决非线性问题。我们之前的公式中有\(<{x _i},{x _j}>\)，他是两个向量的內积，代表着两个样本的相关性。我们把这个叫做核函数。核函数不仅仅是可以为简单的內积，还可以对样本进行多维展开，映射到高维地址空间。这样在低维地址空间线性不可分的样本，在高维空间就变得线性可分了。譬如,\(|x| < 1\)不是线性可分的，但是对其进行\(x \to (x,{x^2})\)映射后，也就的到一个二次曲线，我们可以使用\(y = 1\)进行线性分割。

下面直接引入高斯核函数，它可以对函数进行无线维空间的映射。具体定义如下：

$$k(x,z) = \exp ( - \frac{{||x - z|{|^2}}}{{2{\sigma ^2}}})$$

对于核函数的数学理论和几何意义，以及高斯核为啥可以向无限维空间映射，之后有时间需要详细研究。

我们制造一组\(x _1^2 + x _2^2 = 1\)分割的样本，然后尝试对其进行分割，实际上与上一节程序的区别仅仅在于核函数的选取，这里我们使用高斯核函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
import numpy as np
import random
from matplotlib import pyplot as plt
from matplotlib.patches import Circle


global g_y_vec    # g_y_vec为样本输出, 大小g_m
global g_x_mat    # g_x_mat为样本的输入, 大小2*g_m
global g_m        # g_m 为样本数目
global g_alpha    # g_alpha 大小为g_m
global g_C
global g_w        # 实际没有使用，而是通过alpha表示的
global g_b        # y = wx+b
global g_y_now    # 表示当前参数计算的y，即svmOutPut对应的g_y_now
global g_err      # g_err 表示svmOutput - g_y_vec对应的序列

g_x_mat = np.array([[0.602, 0.732], [-0.599, 0.945], [-0.337, -0.677], [0.459, -0.486], [1.056, 0.137], [0.838, 0.623], [1.022, -0.685], [0.504, 0.821], [-0.977, -0.724], [1.116, 0.56], [0.969, 0.151], [-0.693, 0.077], [1.042, -0.146], [0.705, -0.215], [1.024, -0.322], [1.025, -0.172], [0.306, -1.12], [-0.131, 0.008], [-1.157, -1.081], [0.452, -0.865], [-1.117, -0.533], [-1.083, -0.355], [-0.982, 0.572], [-1.053, 1.003], [-0.553, -0.434], [-0.115, 0.283], [0.785, 0.233], [-0.926, -0.299], [-1.039, 0.581], [0.869, -1.033], [0.754, -1.091], [-1.096, -0.311], [0.537, 0.508], [-0.38, -0.565], [1.165, 0.219], [-0.123, 0.431], [1.048, -0.896], [-0.409, 0.299], [0.537, -0.126], [0.985, -0.577], [-1.135, 1.025], [-0.779, 0.81], [0.547, 0.697], [0.424, -1.015], [0.421, -0.904], [0.151, -0.149], [0.77, -1.011], [-0.401, 1.113], [0.817, 0.573], [0.87, -0.266], [-0.731, 0.418], [-0.651, 0.063], [0.731, 0.04], [0.649, 0.677], [-0.084, -0.568], [0.391, -0.171], [-1.07, 0.738], [-0.307, 0.702], [0.854, 1.125], [0.093, -0.148], [-0.82, 0.969], [0.11, -1.011], [0.672, -0.261], [0.6, -0.262], [0.28, 0.001], [-0.005, -0.544], [-0.666, 0.046], [-0.457, -0.129], [-1.02, 1.071], [1.191, 0.121], [0.665, -0.884], [0.412, 0.665], [-0.992, -1.165], [-0.726, -1.178], [-0.886, 1.08], [0.263, 0.481], [-0.051, 0.668], [0.933, -0.008], [-0.896, -0.637], [-0.605, 0.287], [0.03, -0.232], [0.749, 0.012], [1.175, 0.632], [0.968, 1.106], [-1.19, 0.82], [0.641, 0.129], [-0.375, -1.079], [-0.267, -0.442], [0.361, -0.741], [-0.475, 0.473], [0.133, 1.18], [1.146, 1.185], [-0.293, 0.172], [0.78, -0.805], [0.186, -0.089], [-0.068, 0.829], [-0.621, -0.778], [0.407, -0.523], [0.415, -0.01], [-0.229, 0.002], [-0.997, -0.891], [1.011, -1.186], [0.19, -0.437], [0.958, 0.669], [-0.888, -0.217], [0.444, 0.05], [-0.54, -1.041], [-0.314, 0.296], [0.879, -0.898], [0.127, -0.008], [0.995, -1.11], [-0.878, -0.843], [-0.109, 0.189], [0.859, 0.564], [-0.023, 0.945], [-0.878, 0.899], [-0.062, -1.051], [0.394, 0.519], [-1.139, 0.282], [-0.494, -0.075], [-0.922, 1.11], [0.753, -1.018], [0.816, -1.106], [0.03, 0.569], [-1.11, -0.289], [0.777, 0.025], [0.892, 0.784], [0.91, 0.176], [0.692, 0.099], [0.97, 0.58], [0.034, 1.151], [-0.606, -0.775], [0.873, -0.579], [0.833, -1.042], [-0.251, 0.102], [0.436, -0.585], [0.86, -1.06], [-1.118, 1.094], [0.598, -0.129], [0.694, 0.281], [1.048, -1.036], [-0.348, 0.639], [1.046, -1.124], [-0.333, -0.463], [-0.447, -0.009], [0.344, -0.852], [-1.174, 0.196], [0.701, 0.695], [-0.916, -0.128], [-0.597, -0.934]])
g_y_vec = np.array([1, -1, 1, 1, -1, -1, -1, 1, -1, -1, 1, 1, -1, 1, -1, -1, -1, 1, -1, 1, -1, -1, -1, -1, 1, 1, 1, 1, -1, -1, -1, -1, 1, 1, -1, 1, -1, 1, 1, -1, -1, -1, 1, -1, 1, 1, -1, -1, 1, 1, 1, 1, 1, 1, 1, 1, -1, 1, -1, 1, -1, -1, 1, 1, 1, 1, 1, 1, -1, -1, -1, 1, -1, -1, -1, 1, 1, 1, -1, 1, 1, 1, -1, -1, -1, 1, -1, 1, 1, 1, -1, -1, 1, -1, 1, 1, 1, 1, 1, 1, -1, -1, 1, -1, 1, 1, -1, 1, -1, 1, -1, -1, 1, -1, 1, -1, -1, 1, -1, 1, -1, -1, -1, 1, -1, 1, -1, 1, 1, -1, -1, 1, -1, -1, 1, 1, -1, -1, 1, 1, -1, 1, -1, 1, 1, 1, -1, 1, 1, -1])

def calcLH(id1,id2):
  if g_y_vec[id1] == g_y_vec[id2]:
    L = max(0,g_alpha[id1]+g_alpha[id2]-g_C)
    H = min(g_C,g_alpha[id1]+g_alpha[id2])
  else:
    L = max(0,g_alpha[id2]-g_alpha[id1])
    H = min(g_C,g_C+g_alpha[id2]-g_alpha[id1])
  return (L,H)

def svmOutput(id1):
  # 这个函数是svm的实际输出，计算当前参数(w,b)下, 计算得到的y
  # 由于w = sum (alpha*y*x), 对于第i个分量x_i所以输出结果应该为w*x_i+b, 也就是 sum (alpha*y*<x_1-m,x_i>)
  # 注: 待会分析下alpha的变化趋势与C的关系
  global g_b
  sum = 0;
  for i in range(g_m):
    sum += g_alpha[i]*g_y_vec[i]*kernel(i,id1)
  return sum+g_b

def kernel(id1,id2):
  # 这里核函数为简单的内积
  # id1和id2为int类型，是g_x_mat中的索引
  x_1 = g_x_mat[id1]
  x_2 = g_x_mat[id2]
  val = np.subtract(x_1,x_2)
  val = np.dot(val,val)
  return np.exp(-val)

def compareFun(id1,id2,L,H):
  # 如果返回1，表示L处去极小值。如果返回-1，H处去极小值。如果是0，表示这次不更新
  # 如果两者相等，这里略过, 说明无法有强力证据证明这个样本属于wx+b>1还是wx+b<1，所以等待下一轮迭代。因此，与L和H相等应该设置一个阀值，判断近似相等。
  global g_b
  y_1 = g_y_vec[id1]
  y_2 = g_y_vec[id2]
  e_1 = g_err[id1]
  e_2 = g_err[id2]
  alpha_1 = g_alpha[id1]
  alpha_2 = g_alpha[id2]
  k11 = kernel(id1,id1)
  k12 = kernel(id1,id2)
  k22 = kernel(id2,id2)
  s = y_1*y_2
  f_1 = y_1*(e_1+g_b)-alpha_1*k11-s*alpha_2*k12
  f_2 = y_2*(e_2+g_b)-s*alpha_1*k12-alpha_2*k22
  L_1 = alpha_1+s*(alpha_2-L)
  H_1 = alpha_1+s*(alpha_2-H)
  phi_l = L_1*f_1+L*f_2+0.5*L_1*L_1*k11+0.5*L*L*k22+s*L*L_1*k12
  phi_h = H_1*f_1+H*f_2+0.5*H_1*H_1*k11+0.5*H*H*k22+s*H*H_1*k12
  if L==H:
    return 0
  if phi_l < phi_h:
    return 1
  else:
    return -1

def takeStep(id1,id2,err):
  if id1==id2:
    return 0
  alpha_1 = g_alpha[id1]
  alpha_2 = g_alpha[id2]
  y_1 = g_y_vec[id1]
  y_2 = g_y_vec[id2]
  e1 = g_err[id1]
  e2 = g_err[id2]
  s = y_1*y_2
  L,H=calcLH(id1,id2)
  #print("id1=",id1,", id2=",id2," L=",L,", H=",H)
  if L==H :
    return 0
  k11 = kernel(id1,id1)
  k12 = kernel(id1,id2)
  k22 = kernel(id2,id2)
  eta = k11+k22-2*k12
  #print("kernel:",k11,k12,k22,", eta=",eta,"e1=",e1,"e2=",e2)

  alpha_2_new = alpha_2
  # 如果eta大于0, 我们可知最小值在边界或极小值点上。事实上，如果极小值不在范围内，必在距离极小值近的那个边界上。
  # 如果eta小于0, 我们可知最小值则必在边界上。我们只需要比较两个边界点函数的大小即可。
  if eta>0 :
    alpha_2_new = alpha_2+y_2*(e1-e2)/eta
    alpha_2_new = max(alpha_2_new,L)
    alpha_2_new = min(alpha_2_new,H)
  else:
    # 由于我们知道可以直接这是一个关于alpha的二次函数，并且自变量的取值范围是[L,H], 事实上我们只需要比较alpha_2_new离L和H哪个远即可
    # 但是考虑到eta=0的一次函数特殊情况，我们还是老老实实的计算函数值吧。
    ret = compareFun(id1, id2, L, H)
    if ret == 0:
      alpha_2_new = alpha_2
    elif ret == 1:
      alpha_2_new = L
    elif ret == 1:
      alpha_2_new = H
    print("----------------eta<=0----------------")

  # 归整化alpha_2_new
  if alpha_2_new < err:
    alpha_2_new = 0
  elif alpha_2_new > g_C - err:
    alpha_2_new = g_C
  if abs(alpha_2_new-alpha_2) < err:
    print("alpha_2 is no need to update")
    return 0

  # update b
  global g_b
  alpha_1_new = alpha_1 + s * (alpha_2 - alpha_2_new)      # 不必担心alpha_1_new不在[0,C]范围内，之前的公式已经保证了
  b1_new = -e1-y_1*k11*(alpha_1_new-alpha_1)-y_2*k12*(alpha_2_new-alpha_2) + g_b
  b2_new = -e2-y_1*k12*(alpha_1_new-alpha_1)-y_2*k22*(alpha_2_new-alpha_2) + g_b
  if alpha_1_new>0 and not alpha_1_new<g_C:
    g_b = b1_new
  elif alpha_2_new>0 and not alpha_2_new<g_C:
    g_b = b2_new
  else:
    g_b = 0.5*(b1_new+b2_new)

  # update alpha
  g_alpha[id1] = alpha_1_new
  g_alpha[id2] = alpha_2_new
  print("g_alpha[id1]=",g_alpha[id1],"g_alpha[id2]=",g_alpha[id2],"s=",s,", alpha_1=",alpha_1,", alpha_2=",alpha_2)

  # update err g_y_now
  updateYAndErr()

  return 1

def updateYAndErr():
  for i in range(g_m):
    g_y_now[i] = svmOutput(i)
    g_err[i] = svmOutput(i)-g_y_vec[i]

def chooseBestAlphaIndex(id2):
  maxIncr = 0
  maxIndex = -1;
  for i in range(g_m):
    incr = abs(g_err[i]-g_alpha[i])
    if incr >= maxIncr:
      maxIndex = i
      maxIncr = incr
  return maxIndex

def sizeOfNonZerorAndNonC():
  size=0
  for i in range(g_m):
    if g_alpha[i]!=0 and g_alpha[i]!=g_C:
      size= size+1
  return size

def chooseRandomIndex(id2):
  ret = id2;
  while ret==id2:
    ret = random.randint(0,g_m-1)
  return ret

# 对于examineExample函数,我们一次进选择id2样本对应的alpha与如下规则选择的id1对应的alpha,然后相应跟新其值。
def examineExample(id2):
  y_2 = g_y_vec[id2]
  tol = 1e-2        # 是一个正数
  alpha_2 = g_alpha[id2]
  e_2 = svmOutput(id2)-g_y_vec[id2]
  r_2 = e_2 * y_2

  # 我们只对当前违反kkt条件的样本对应的alpha进行更新
  # 关于违反kkt条件的说明:
  # (1) r_2 < -tol 表示r_2小于0，即表示输出的预测结果与样本的y符号相反，因此应该属于误差案例的。所以，根据公式，alpha = C。如果alpha < C ,比违反kkt条件
  # (2) r_2 < -tol 表示r_2大于0，即表示输出的预测结果与样本的y符号相同，当误差大于一定的
  if r_2 < -tol and alpha_2 < g_C or r_2 > tol and alpha_2 > 0 :
    # 下面的程序逻辑是这样的:
    # 先遍历alpha非0或非C, 因为我们对于alpha为0和alpha为C的情况, 认为是处于非支持向量和处于误差样本的情况。我们只有根据支持向量下，找到最优的||w||才有意义
    # 首先，我们找到|e1-e2|最大的alpha, 从这里优化。如果优化结果不理想，我们就随机找一个alpha一起计算。如果还不行，就在整个范围alpha范围内计算
    if sizeOfNonZerorAndNonC()>0:
      id1=chooseBestAlphaIndex(id2)
      if takeStep(id1,id2,1e-3):
        #print("takeStep1, alpha[",id1,"]=",g_alpha[id1],", alphapp[",id2,"]=",g_alpha[id2])
        return 1
    r=chooseRandomIndex(id2)
    for i in range(g_m):
      id1 = (r+i)%g_m
      if id1!=id2 and g_alpha[id1]!=0 and g_alpha[id1]!=g_C:
        if takeStep(id1,id2,1e-3):
          #print("takeStep2, alpha[", id1, "]=", g_alpha[id1], ", alphapp[", id2, "]=", g_alpha[id2])
          return 1
    r = chooseRandomIndex(id2)
    for i in range(g_m):
      id1 = (r + i) % g_m
      if id1 != id2:
        if takeStep(id1,id2,1e-3):
          #print("takeStep3, alpha[", id1, "]=", g_alpha[id1], ", alphapp[", id2, "]=", g_alpha[id2])
          return 1
  return 0

def kernel_test(id1,x):
  # 这里核函数为简单的内积
  # id1和id2为int类型，是g_x_mat中的索引
  x_1 = g_x_mat[id1]
  val = np.subtract(x_1,x)
  val = np.dot(val,val)
  return np.exp(-val)

def svmOutput_test(alpha,b,x):
  # 这个函数是svm的实际输出，计算当前参数(w,b)下, 计算得到的y
  # 由于w = sum (alpha*y*x), 对于第i个分量x_i所以输出结果应该为w*x_i+b, 也就是 sum (alpha*y*<x_1-m,x_i>)
  # 注: 待会分析下alpha的变化趋势与C的关系
  global g_m
  sum = 0
  for i in range(g_m):
    if alpha[i]!=0:
      sum += alpha[i]*g_y_vec[i]*kernel_test(i,x)
  return sum+\
         b

def showPic(alpha,b):
  figure, ax = plt.subplots()
  ax.set_xlim(left=-2, right=2)
  ax.set_ylim(bottom=-2, top=2)

  # 生成100组测试数据
  x=[]
  for j in range(100):
    x_0 = random.randint(-1200,1200)/1000
    x_1 = random.randint(-1200,1200)/1000
    x.append([x_0,x_1])

  for i in range(100):
    if svmOutput_test(alpha,b,x[i])>0:
      plt.plot(x[i][0], x[i][1], 'b--', marker='+', color='r')
    else:
      plt.plot(x[i][0], x[i][1], 'b--', marker='o', color='b')

  # draw x_0*x_0+x_1*x_1=0
  cir1 = Circle(xy=(0.0, 0.0), radius=1)
  ax.add_patch(cir1)

  plt.xlabel("x1")
  plt.ylabel("x2")
  plt.plot()
  plt.show()

if __name__=="__main__":
  SHOW_PIC = True

  g_m = len(g_x_mat)
  if SHOW_PIC == False:
    # 1 training
    g_alpha = np.zeros(g_m)
    g_y_now = np.zeros(g_m)
    g_err = np.zeros(g_m)
    global g_b
    g_b = 0
    numChanged = 0
    examineAll = 1
    g_C = 10
    err = 0
    updateYAndErr()       # 实现更新下缓冲，即当前输出与误差值
    while numChanged>0 or examineAll:
      numChanged = 0
      # 循环处理，第一次对所有的样本进行一次处理。
      # 然后对所有非边界的数值进行处理。因为在当前参数下，非边界的样本，我们认为其是支持向量。对于优化||w||的大小，支持向量才有意义。
      if examineAll:
        for i in range(g_m):
          numChanged += examineExample(i)
          #print("examineAll=1, numChanged=",numChanged)
      else:
        for i in range(g_m):
          if g_alpha[i]!=0 and g_alpha[i]!=g_C:
            numChanged += examineExample(i)
      examineAll = abs(examineAll-1)
    print(g_alpha, g_b)
  else:
    # 3 show
    alpha= [  0.00000000e+00,   7.59410972e-01,  -2.22044605e-16,   0.00000000e+00,
    1.00000000e+01,   1.00000000e+01,   0.00000000e+00,   0.00000000e+00,
    0.00000000e+00,   0.00000000e+00,   1.00000000e+01,   0.00000000e+00,
    5.67018243e+00,   0.00000000e+00,   0.00000000e+00,   1.00000000e+01,
    0.00000000e+00,   0.00000000e+00,   0.00000000e+00,   1.00000000e+01,
    0.00000000e+00,   2.45788486e+00,   1.33286169e+00,   0.00000000e+00,
    0.00000000e+00,   0.00000000e+00,   1.11022302e-16,   1.00000000e+01,
    0.00000000e+00,   0.00000000e+00,   0.00000000e+00,   7.22541284e+00,
    0.00000000e+00,  -1.38777878e-17,   0.00000000e+00,  -2.77555756e-17,
    0.00000000e+00,   0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
    0.00000000e+00,   8.66273771e-04,   0.00000000e+00,   8.33442222e+00,
    1.00000000e+01,   0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
    1.00000000e+01,   1.00000000e+01,  -2.77555756e-17,   0.00000000e+00,
    0.00000000e+00,   0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
    0.00000000e+00,   0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
    0.00000000e+00,   1.00000000e+01,   0.00000000e+00,   0.00000000e+00,
    0.00000000e+00,   0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
    0.00000000e+00,   0.00000000e+00,   4.39461998e+00,   0.00000000e+00,
    0.00000000e+00,   0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
    0.00000000e+00,   1.00000000e+01,   1.00000000e+01,   0.00000000e+00,
    0.00000000e+00,   0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
    0.00000000e+00,   0.00000000e+00,  -2.22044605e-16,   0.00000000e+00,
    0.00000000e+00,   0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
    0.00000000e+00,   0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
    1.00000000e+01,   0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
    0.00000000e+00,   0.00000000e+00,   0.00000000e+00,  -2.77555756e-17,
    0.00000000e+00,   0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
    -5.55111512e-17,  0.00000000e+00,   0.00000000e+00,   6.59194921e-17,
    0.00000000e+00,   1.00000000e+01,   1.00000000e+01,  -1.38777878e-17,
    5.21868376e+00,   0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
    0.00000000e+00,   0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
    0.00000000e+00,   0.00000000e+00,  -2.22044605e-16,   6.56986459e+00,
    0.00000000e+00,   5.19744490e+00,   9.69510083e+00,   1.00000000e+01,
    1.00000000e+01,   0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
    0.00000000e+00,   0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
    0.00000000e+00,   0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
    0.00000000e+00,   8.69782724e+00,   0.00000000e+00,   1.00000000e+01,
    3.24960991e+00,   8.23041098e+00]
    b = -2.68518972087
    #w = np.array([0, 0])
    #for i in range(g_m):
    #  if g_alpha[i] != 0:
    #    w = np.add(w, g_y_vec[i] * g_alpha[i] * g_x_mat[i])
    showPic(alpha,b)

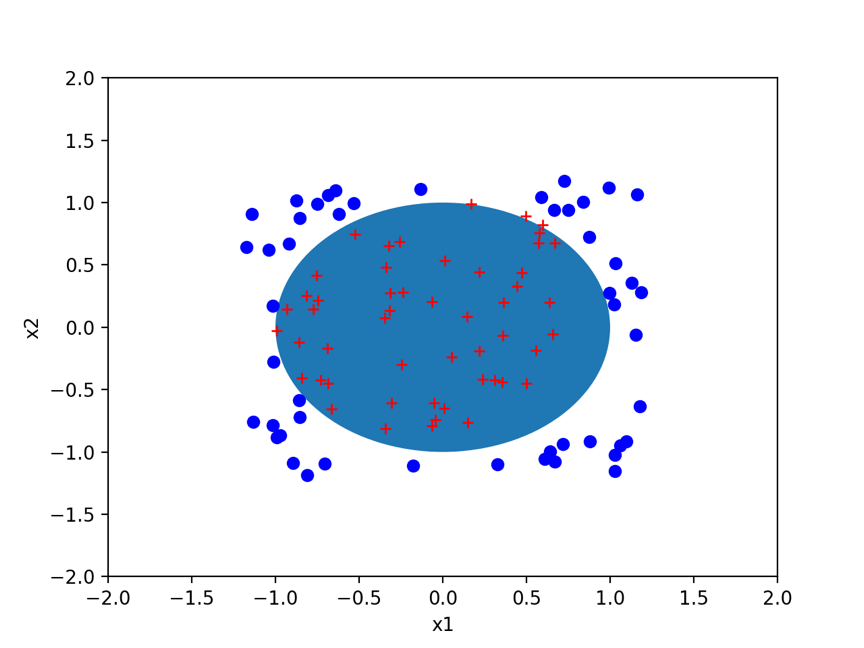
经过数轮迭代之后，得到参数。然后在随机产生一些样本，通过训练集得到参数对随机测试样本进行分割，结果如下，发现分割效果还是很理想的。

附录

手写公式和word版博客地址:

1
https://github.com/zhengchenyu/MyBlog/tree/master/doc/mlearning/支持向量机

参考文献