机器学习-3.1-非监督学习之聚类.md

聚类问题

本节主要介绍非监督学习的聚类算法。

1 常见的聚类算法

聚类问题中，我们给定训练集合\(\{ {x{(1)}},{x{(2)}},…,{x^{(m)}}\}\)，目的是将训练样本聚合几个类中。由于问题过程中，\(y\)并没有指定，所以这是一个非监督问题。

1.1 k-means

下面介绍k-means算法。算法的主要流程如下：

  • (1) 随机初始化重心\(\{ {x{(1)}},{x{(2)}},…,{x^{(m)}}\}\)(假设有k个分类)
  • (2) 根据当前的\(\{ {x{(1)}},{x{(2)}},…,{x^{(m)}}\}\)，计算距离每个样本距离最近的中心，即为所属类。
  • (3) 然后根据2中得到新的所属类关系，更新一组新的重心值。
  • (4) 重复2,3直到某个截止条件。

下面我们随机制造以三个点为高斯分布的一组数据，试图从该组数据完成聚类操作，具体代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
import numpy as np
from matplotlib import pyplot as plt
import sys

def makeData():
  # 0 make data
  mean_1 = [1, 1]
  mean_2 = [2, 2]
  mean_3 = [1, 2]
  cov = [[0.05, 0], [0, 0.05]]
  arr1 = np.random.multivariate_normal(mean_1, cov, 100)
  arr2 = np.random.multivariate_normal(mean_2, cov, 50)
  arr3 = np.random.multivariate_normal(mean_3, cov, 50)
  figure, ax = plt.subplots()
  ax.set_xlim(left=-1, right=4)
  ax.set_ylim(bottom=-1, top=4)
  for i in range(len(arr1)):
    plt.plot(arr1[i][0], arr1[i][1], 'b--', marker='+', color='r')
  for i in range(len(arr2)):
    plt.plot(arr2[i][0], arr2[i][1], 'b--', marker='o', color='g')
  for i in range(len(arr3)):
    plt.plot(arr3[i][0], arr3[i][1], 'b--', marker='*', color='b')
  plt.xlabel("x1")
  plt.ylabel("x2")
  return np.vstack((arr1,arr2,arr3))

def updateSingleLabel(x,center):
  n = len(center)
  min = sys.maxsize
  minIndex = -1
  for i in range(n):
    tmp = np.linalg.norm(x - center[i])
    if tmp < min:
      minIndex=i
      min = tmp
  return minIndex

def updateLable(data,label,center):
  numChanged = 0;
  n=len(data)
  label_new = np.zeros(n);
  for i in range(n):
    label_new[i] = updateSingleLabel(data[i], center)
    if label_new[i] != label[i]:
      numChanged = numChanged + 1
  for i in range(n):
    label[i] = label_new[i]
  return numChanged;

def updateCenter(data,label,center):
  newCenter=np.array([[0.0,0.0],[0.0,0.0],[0.0,0.0]])
  newCenterSum=np.array([0,0,0])
  for i in range(len(data)):
    if label[i]==0:
      newCenter[0] = newCenter[0] + data[i]
      newCenterSum[0] = newCenterSum[0] + 1
    elif label[i] == 1:
      newCenter[1] = newCenter[1] + data[i]
      newCenterSum[1] = newCenterSum[1] + 1
    elif label[i] == 2:
      newCenter[2] = newCenter[2] + data[i]
      newCenterSum[2] = newCenterSum[2] + 1
  if newCenterSum[0] > 0 :
    center[0] = newCenter[0]/newCenterSum[0]
  if newCenterSum[1] > 0 :
    center[1] = newCenter[1]/newCenterSum[1]
  if newCenterSum[2] > 0 :
    center[2] = newCenter[2]/newCenterSum[2]

def showPic(x,label,label1):
  figure, ax = plt.subplots()
  ax.set_xlim(left=-1, right=4)
  ax.set_ylim(bottom=-1, top=4)
  for i in range(len(x)):
    if label[i] == 0:
      plt.plot(x[i][0], x[i][1], 'b--', marker='+', color='r')
    elif label[i] == 1:
      plt.plot(x[i][0], x[i][1], 'b--', marker='o', color='g')
    elif label[i] == 2:
      plt.plot(x[i][0], x[i][1], 'b--', marker='*', color='b')
  figure, ax = plt.subplots()
  ax.set_xlim(left=-1, right=4)
  ax.set_ylim(bottom=-1, top=4)
  for i in range(len(x)):
    if label1[i] == 0:
      plt.plot(x[i][0], x[i][1], 'b--', marker='+', color='r')
    elif label1[i] == 1:
      plt.plot(x[i][0], x[i][1], 'b--', marker='o', color='g')
    elif label1[i] == 2:
      plt.plot(x[i][0], x[i][1], 'b--', marker='*', color='b')
  plt.show()

if __name__=="__main__":

  # 0 make data
  data=makeData()

  # 1 initial
  n = len(data)
  label = np.zeros(n)       # 0,1,2 represent center[0],center[1],center[2]
  center = np.array([[0.0,3.0],[3.0,3.0],[0.0,0.0]])
  label1 = np.zeros(n)
  center1 = np.array([[0.0,10.0],[2.0,3.0],[0.5,5.0]])

  # 2. trainning
  # 2.1 trainning for good initial
  while True:
    # update label
    numChanged = updateLable(data,label,center)
    # update center
    updateCenter(data,label,center)
    if numChanged==0:
      break

  # 2.1 trainning for bad initial
  while True:
    # update label
    numChanged = updateLable(data,label1,center1)
    # update center
    updateCenter(data,label1,center1)
    if numChanged==0:
      break

  # 3. showData
  showPic(data,label,label1)

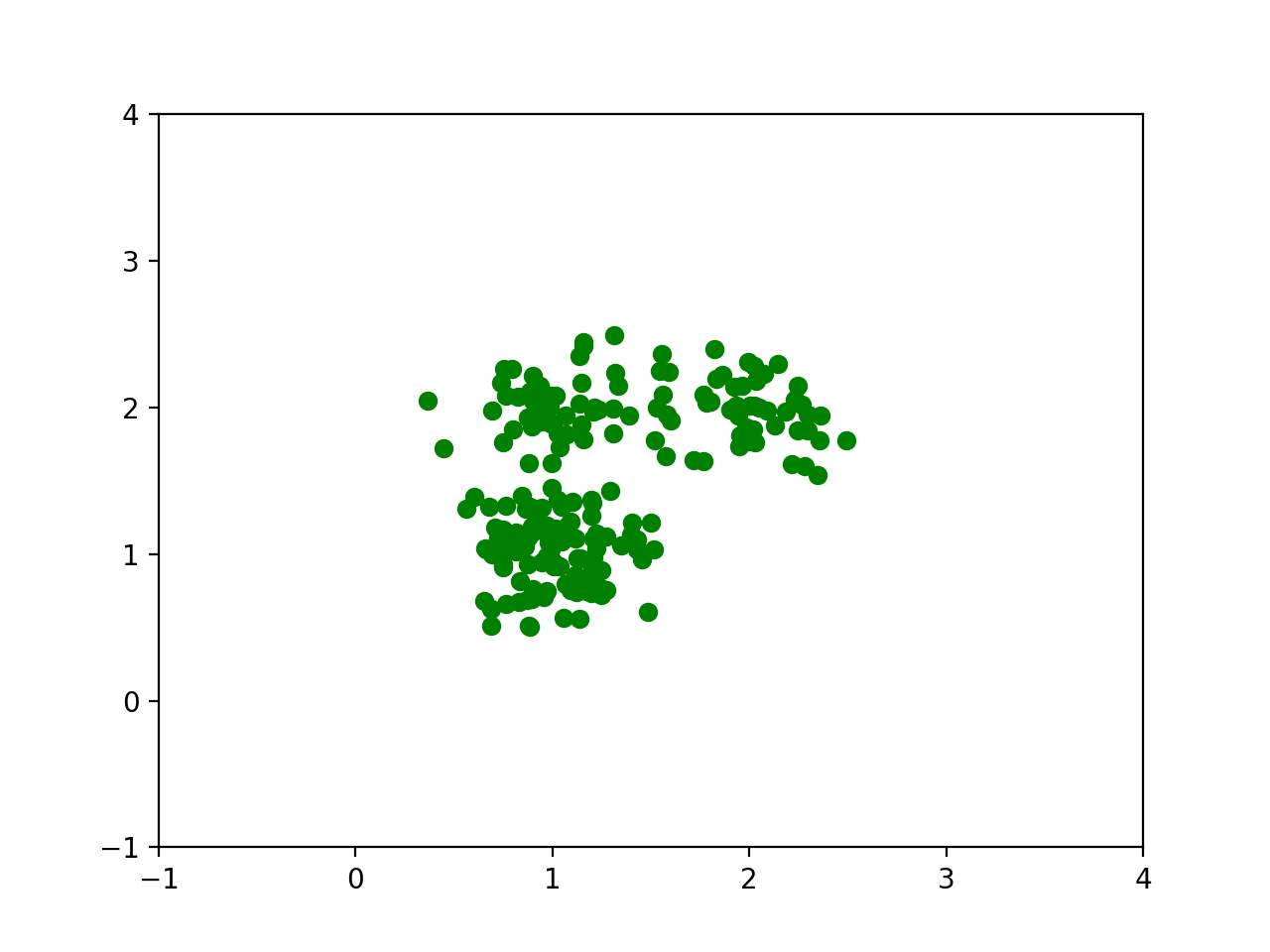
下面是随机产生的基于(1，1),(2，2),(1,2)的高斯分布。

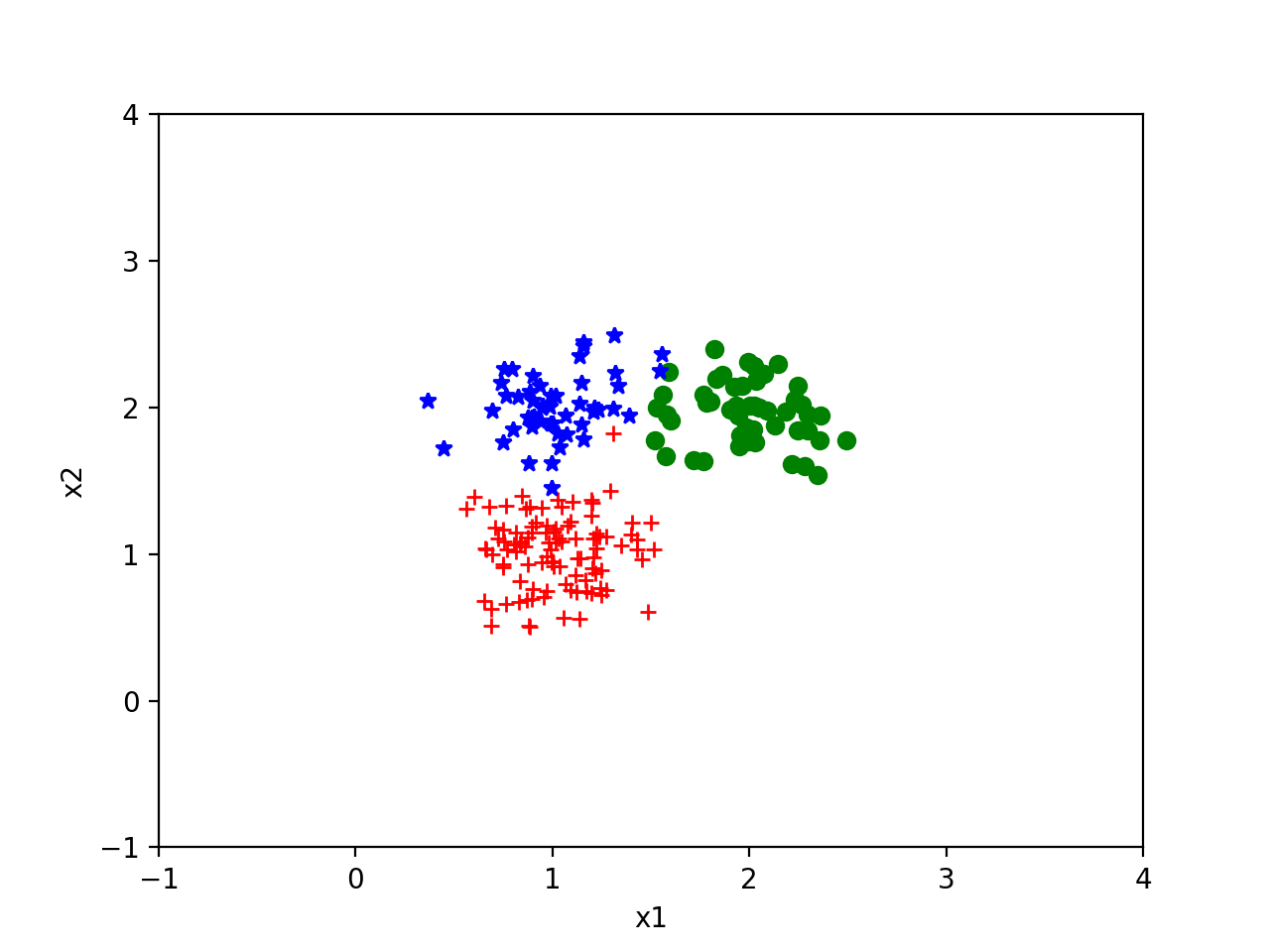
然后我们从(0.0,3.0),(3.0,3.0),(0.0,0.0)开始迭代得到如下效果，可以看出结果还是非常理想的。

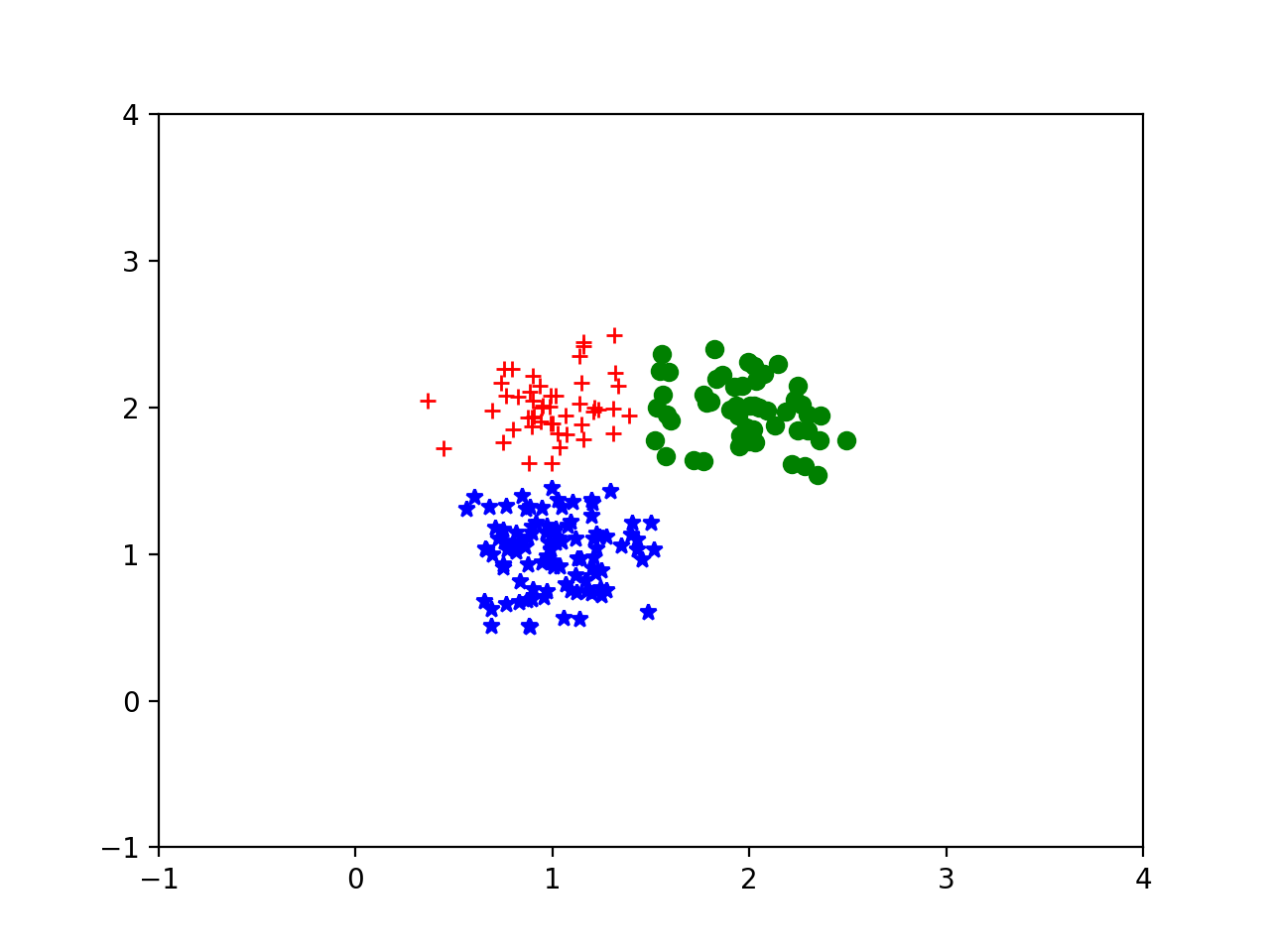
然后我们试图从(0.0,10.0),(2.0,3.0),(0.5,5.0)开始迭代,则会得到这样的结果。

可以从上文中看出，k-means对初始值的敏感度很高。对于现实问题，也许我们并不知道训练样本中本身存在多个分类，我们可以设置多个分类，如果某一个分类里面的样本过少，就删除分类，这样就不再依赖于事先知道分类的数量了。

1.2 高斯混合聚类

假设我们的分类都服从于各自的高斯分布，我们试图从样本中对其分类。该问题与之前的高斯判别分析类似，区别仅仅在于该问题没有样本标签。
我们设置z表示样本的距离分类，可以知道他服从一个多项式分布, \({z^{(i)}} \sim Multinomial(\phi )\)，其中。然后已经\(z\)之后，\(x\)服从的是一个高斯分布，\({x{(i)}}|{z{(i)}} = j \sim N({\mu _j},{\Sigma _j})\)。

下面直接写出算法过程(具体的算法推导见EM算法小节)：

  • (1) 随机初始化\(\phi\),\(\mu\),\(\Sigma\)。
  • (2) 遍历样本，计算得\([w _j^{(i)}\),如下：
$$w _j^{(i)} = p({z^{(i)}} = j|{x^{(i)}},\phi ,\mu ,\Sigma )$$ $$w _j^{(i)} = p({z^{(i)}} = j|{x^{(i)}},\phi ,\mu ,\Sigma ) = \frac{{p({z^{(i)}} = j,{x^{(i)}})}}{{p({x^{(i)}})}} = \frac{{p({z^{(i)}} = j,{x^{(i)}})}}{{\sum\limits _{j = 1}^k {p({x^{(i)}},{z^{(i)}} = j)} }}$$
  • (3) 根据计算得到的\(w\)重新更新各个分类的分布，如下：
$${\phi _j} = \frac{1}{m}\sum\limits _{i = 1}^m {1\{ {z^{(i)}} = j\} } $$ $${\mu _j} = \frac{{\sum\limits _{i = 1}^m {1\{ {z^{(i)}} = j\} } {x^{(i)}}}}{{\sum\limits _{i = 1}^m {1\{ {z^{(i)}} = j\} } }}$$ $${\Sigma _j} = \frac{{\sum\limits _{i = 1}^m {1\{ {z^{(i)}} = j\} } ({x^{(i)}} - {\mu _j}){{({x^{(i)}} - {\mu _j})}^T}}}{{\sum\limits _{i = 1}^m {1\{ {z^{(i)}} = j\} } }}$$
  • (4) 重复2,3知道达到截止条件。

下面我们制作一组由三个高斯分布组成的样本数据，对其进行聚类。代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
# coding=utf-8
import numpy as np
from matplotlib import pyplot as plt
from scipy.stats import multivariate_normal

def make_data():
  mean_1 = [1,1]
  mean_2 = [4,4]
  mean_3 = [1,4]
  cov1 = [[0.1,0],[0,0.1]]
  cov2 = [[0.2,0],[0,0.2]]
  cov3 = [[0.6,0],[0,0.6]]
  arr1 = np.random.multivariate_normal(mean_1, cov1, 100)
  arr2 = np.random.multivariate_normal(mean_2, cov2, 50)
  arr3 = np.random.multivariate_normal(mean_3, cov3, 50)
  figure, ax = plt.subplots()
  ax.set_xlim(left=-4, right=8)
  ax.set_ylim(bottom=-4, top=8)
  for i in range(len(arr1)):
    plt.plot(arr1[i][0], arr1[i][1], 'b--', marker='+', color='r')
  for i in range(len(arr2)):
    plt.plot(arr2[i][0], arr2[i][1], 'b--', marker='o', color='g')
  for i in range(len(arr3)):
    plt.plot(arr3[i][0], arr2[i][1], 'b--', marker='*', color='b')
  plt.xlabel("x1")
  plt.ylabel("x2")
  plt.plot()
  plt.title("sample")
  #plt.show()
  return np.vstack((arr1, arr2, arr3))

def updatePhi(w):
  n1 = len(w)
  phi=np.zeros(n1)
  for i in range(n1):
    sum = 0
    n2 = len(w[i])
    for j in range(n2):
      sum = sum + w[i][j]
    phi[i] = sum/n2
  return phi

def updateW(data,w,phi,mu,sigma):
  n1=len(w)           # 3
  n2 = len(w[0])      # 200
  var = []
  for k in range(n1):
    var.append(multivariate_normal(mean=mu[k].tolist(), cov=sigma[k].tolist()))

  for j in range(n2):
    sum = 0
    for i in range(n1):
      sum = sum + var[i].pdf(data[j])*phi[i]
    for i in range(n1):
      w[i][j] = var[i].pdf(data[j])*phi[i]/sum

def updateMu(data,w,mu):
  changed=False
  n1 = len(w)  # 3
  n2 = len(w[0])  # 200
  for i in range(n1):
    sumW = 0.0
    sumX = np.array([0.0,0.0])
    for j in range(n2):
      sumW = sumW + w[i][j]
      sumX = sumX + w[i][j]*data[j]
    mu_new = sumX / sumW
    if np.dot(mu_new-mu[i],mu_new-mu[i]) > 0.001:
      changed = True
    mu[i] = mu_new
  return changed

def updateSigma(data,w,mu,sigma):
  n1 = len(w)  # 3
  n2 = len(w[0])  # 200
  sum=np.array([[0,0],[0,0]])
  for i in range(n1):
    sumW = 0.0
    sumX = np.array([0.0,0.0])
    for j in range(n2):
      sumW = sumW + w[i][j]
      z0 = np.array([data[j] - mu[i]])
      z0T = np.array([data[j] - mu[i]]).transpose()
      sumX = sumX + w[i][j]*np.dot(z0T, z0)
    sigma[i] = sumX/sumW

def classify(data,mu,sigma):
  n1=len(w)           # 3
  n2 = len(w[0])      # 200
  var=[]
  for k in range(n1):
    var.append(multivariate_normal(mean=mu[k].tolist(), cov=sigma[k].tolist()))

  figure, ax = plt.subplots()
  ax.set_xlim(left=-4, right=8)
  ax.set_ylim(bottom=-4, top=8)

  for i in range(n2):
    tmp_arr=np.array([])
    for j in range(n1):
      tmp_arr=np.append(tmp_arr,var[j].pdf(data[i]))
    index = tmp_arr.argmax()
    if index == 0:
      plt.plot(data[i][0], data[i][1], 'b--', marker='+', color='r')
    elif index == 1:
      plt.plot(data[i][0], data[i][1], 'b--', marker='o', color='g')
    elif index == 2:
      plt.plot(data[i][0], data[i][1], 'b--', marker='o', color='b')
  plt.xlabel("x1")
  plt.ylabel("x2")
  plt.title("result")
  plt.plot()
  plt.show()

if __name__ == "__main__":
  # 1 make data
  classN=3
  data=make_data()
  n=len(data)
  for k in range(n):
    w = np.array([np.zeros(n), np.zeros(n), np.zeros(n)])
  # w = array[classN][n] =array[3][200]
  for i in range(classN):
    for j in range(n):
      w[i][j]= 1.0/classN

  phi=updatePhi(w)
  mu = np.array([[6.0, 6.0], [4.0, -1.0], [-2.0, 2.0]])
  sigma=np.array([[[0.1,0],[0,0.1]],[[0.1,0],[0,0.1]],[[0.1,0],[0,0.1]]])

  # 2 training
  while True:
    updateW(data,w,phi,mu,sigma)
    updatePhi(w)
    updateSigma(data,w,mu,sigma)
    changed = updateMu(data,w,mu)
    if changed == False:
      print("迭代完成")
      break

  # 3 show
  print("mu=",mu,", sigma=",sigma)
  classify(data,mu,sigma)

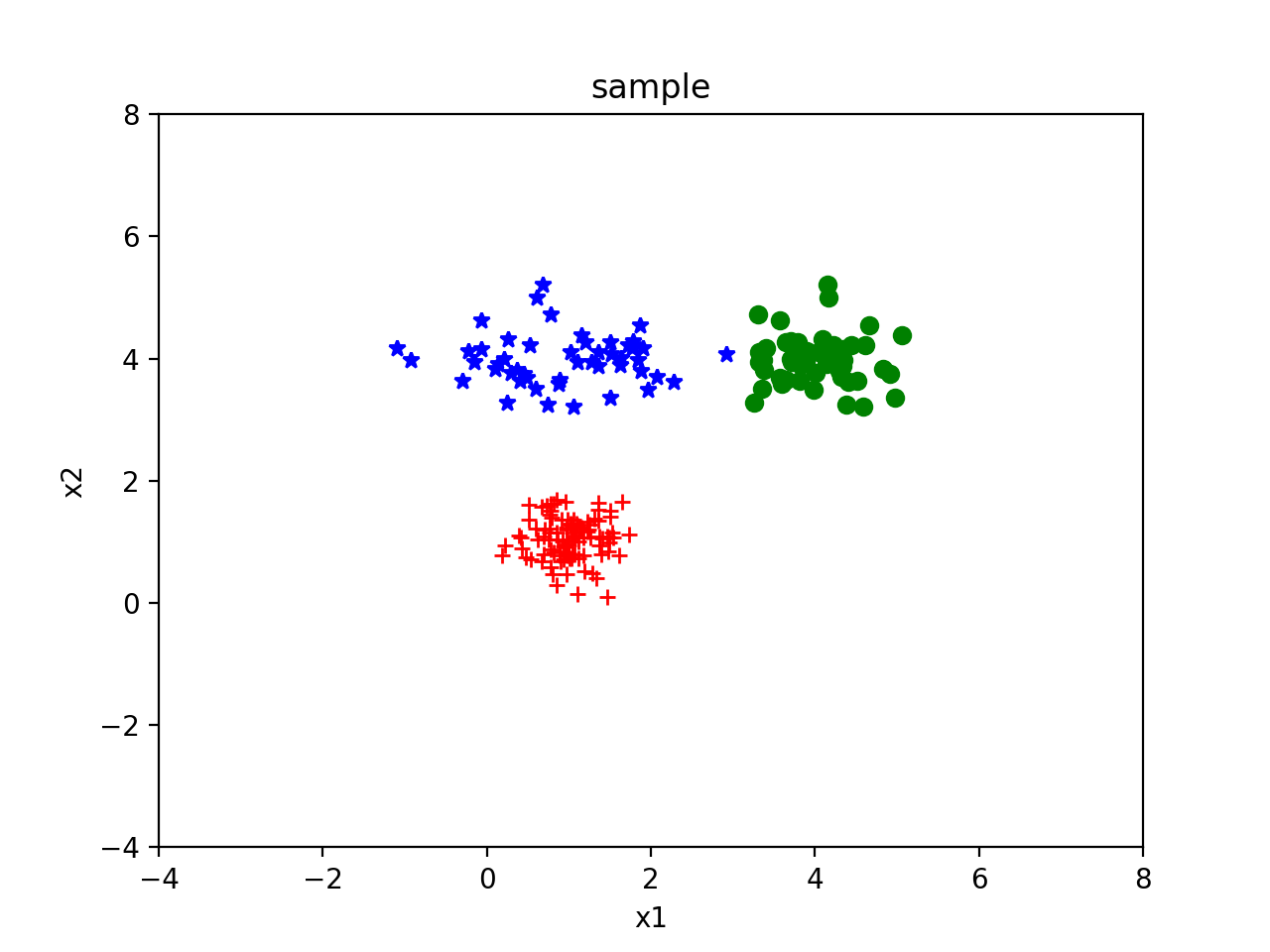
我们分别以[6.0, 6.0], [4.0, -1.0], [-2.0, 2.0]为均值，以[[0.1,0],[0,0.1]],[[0.1,0],[0,0.1]],[[0.1,0],[0,0.1]]为标准差生成一组高斯分布如下：

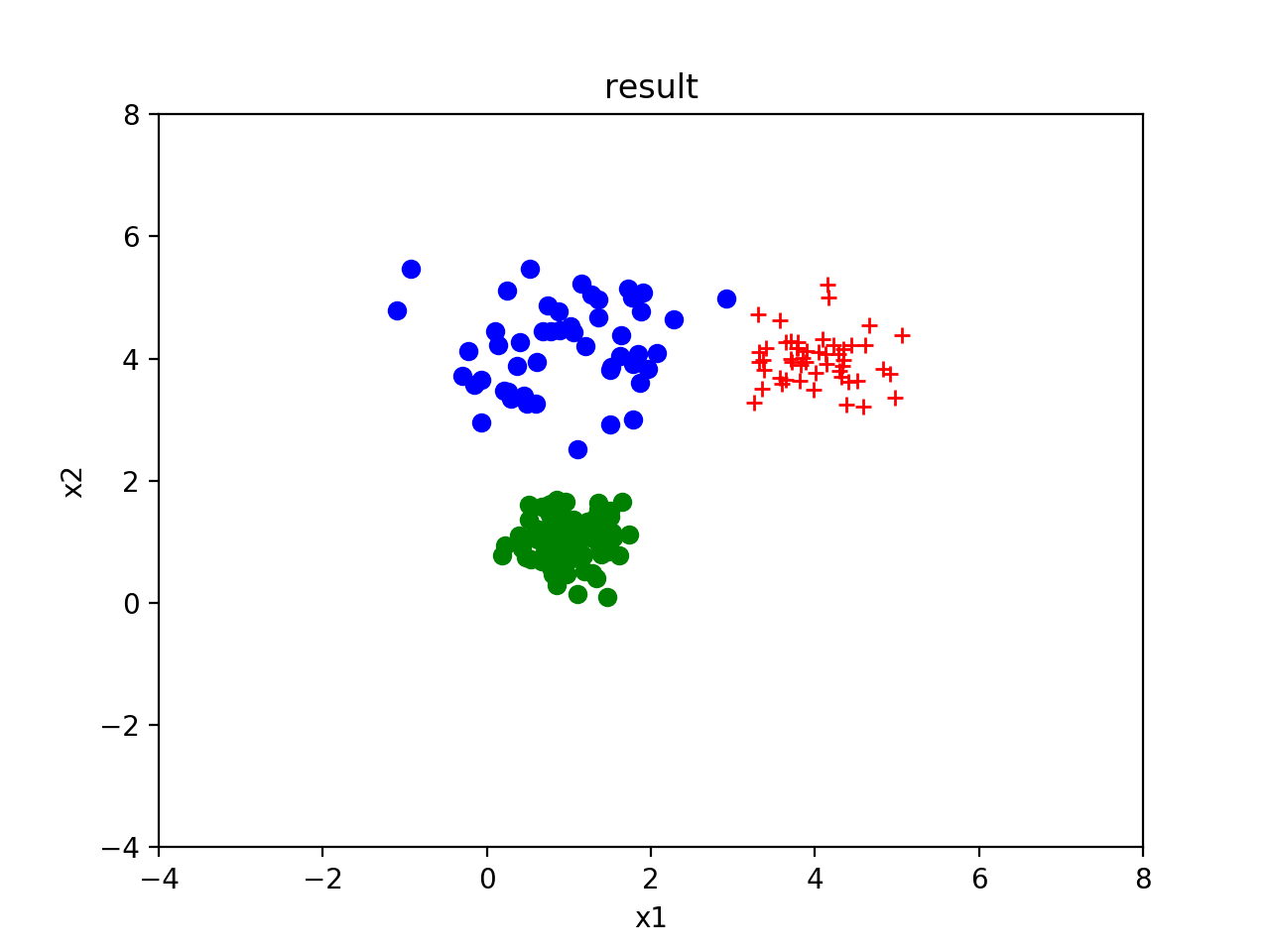
然后通过训练的到的训练均值分别为[4.00729834, 3.99848889], [1.01089497, 1.05225006], [0.92949217, 4.18380895]]。标准差为[[0.23196114,-0.01896477],[-0.01896477, 0.17165715]], [[0.10205901, 0.00157192], [0.00157192, 0.11477843]], [[0.7010517, 0.04783335], [0.04783335, 0.51147277]]。具体结果如下:

### 2.1 Jensen不等式 对于一个严格凸函数,即\\(f''(x) \geqslant 0\\)，我们容易得到下式: $$E[f(x)] \geqslant f(E[x])$$

当且仅当x为常数的时候，上式等号成立。对于严格凹函数，则正好相反。

2.2 EM算法模型建立

假定我们的数据有\(k\)个分类。我们聚类的目标是，样本在自己分类中出现的概率最大。或者换句话说，让其在所属分类的分布(可以用高斯分类假想该问题)中出现的概率最大。可是对于非监督学习问题，我们不知道具体的分类。因此，我们可以将模型假定为找到给定参数\(\theta\)对应分布，是的\(x\)在分布中出现的概率足够大，这说明(\theta\)对应的分布能够充分的表示某一组分类。因此可以构造如下的最大释然函数：

$$\ell (\theta ) = \sum\limits _{i = 1}^m {\ln p({x^{(i)}};\theta )} $$

进入推导最大释然函数：

$$\ell (\theta ) = \sum\limits _{i = 1}^m {\ln \sum\limits _{j = 1}^k {p({x^{(i)}},{z^{(j)}};\theta )} } = \sum\limits _{i = 1}^m {\ln \sum\limits _{j = 1}^k {{Q _i}({z^{(i)}} = j)\frac{{p({x^{(i)}},{z^{(i)}} = j;\theta )}}{{{Q _i}({z^{(i)}} = j)}}} } $$

上面\(k\)为分类的个数。对上面的\({Q _i}\)为一个概率分布，有:

$$\sum\limits _{j=1} ^k {{Q _i}({z^{(i)}}=j)}=1$$

对于\(f(x) = \ln x\),我们知道\(f’'(x) = - \frac{1}{x^2}\),可知其为一个严格凹函数。上式可以写成：

$$\ell (\theta ) = \sum\limits _{i = 1}^m {f(E[\frac{{p({x^{(i)}},{z^{(i)}} = j;\theta )}}{{{Q _i}({z^{(i)}} = j)}}])}$$

根据Jensen不等式，我们有:

$$\ell (\theta ) = \sum\limits _{i = 1}^m {f(E[\frac{p({x^{(i)},{z^{(i)}};\theta )}}{{Q _i}({z^{(i)}} = j)}])} \geqslant \sum\limits _{i = 1}^m {E[f(\frac{p({x^{(i)}},{z^{(i)}} = j;\theta )}{{Q _i}({z^{(i)}} = j)})]} = \sum\limits _{i = 1}^m {\sum\limits _{j = 1}^k {{Q _i}({z^{(i)}} = j)\ln (\frac{p({x^{(i)}},{z^{(i)}} = j;\theta )}{{Q _i}({z^{(i)}} = j)})} }$$

因此我们得到最大释然函数的下确定，即为上式子中后面的部分。我们只要保证下确定随着迭代的方向单调递增即可，具体的要保证\(\ell ({\theta ^{(t + 1)}}) \geqslant \ell ({\theta ^{(t)}})\)。这里我们设\(low(\theta )\)是已知\({Q _i}\)的情况下，最大释然函数的下确定关于\(\theta\)的函数。我们看如下公式:

$$\ell ({\theta ^{(t + 1)}}) \geqslant low({\theta ^{(t + 1)}}) \geqslant low({\theta ^{(t)}}) = \ell ({\theta ^{(t)}})$$

事实上，我们只要保证上面的式子我们就可以保证迭代方向是正确的。其中，第一个不等号是必然成立的。那我们分头来构造条件是后面的式子成立。
首先如果保证最后一个等号的成立，根据Jensen不等式，只有自变量为常数才能事等号成立，这样我们设置如下式子(其中\(c\)为常数):

$$\frac{{p({x^{(i)}},{z^{(i)}} = j;\theta )}}{{{Q _i}({z^{(i)}} = j)}} = c$$

然后对上面的式子按照分类累积求和得:

$$\sum\limits _{j = 1}^k {p({x^{(i)}},{z^{(i)}} = j;\theta )} = c\sum\limits _{j = 1}^k {{Q _i}({z^{(i)}} = j)} = c$$

因此得:

$${Q _i}({z^{(i)}} = j) = \frac{{p({x^{(i)}},{z^{(i)}} = j;\theta )}}{{\sum\limits _{j = 1}^k {p({x^{(i)}},{z^{(i)}} = j;\theta )} }} = p({z^{(i)}}|{x^{(i)}};\theta)$$

这样我们完成EM算法的E步骤。然后解决中间大于等于号的问题。这个就比较好解决了，我们只需要计算下确定函数关于\(\theta\)求最大值，最大值对应的参数，可保证不等号的成立，即为迭代的正确方向。具体公式如下：

$$\theta = \arg {\max _\theta }\sum\limits _{i = 1}^m {\sum\limits _{j = 1}^k {{Q _i}({z^{(i)}} = j)\ln \frac{{p({x^{(i)}},{z^{(i)}} = j;\theta )}}{{{Q _i}({z^{(i)}} = j)}}} }$$

综上，我们来重新整理一下EM算法，具体如下：

  • (1) 初始化相关参数
  • (2) E步骤:计算\({Q _i}\)，如下：
$${Q _i}({z^{(i)}} = j) = p({z^{(i)}}|{x^{(i)}};\theta)$$
  • (3) M步骤：更新参数\(\theta\)，如下：
$$\theta = \arg {\max _\theta }\sum\limits _{i = 1}^m {\sum\limits _{j = 1}^k {{Q _i}({z^{(i)}} = j)\ln \frac{{p({x^{(i)}},{z^{(i)}} = j;\theta )}}{{{Q _i}({z^{(i)}} = j)}}} } $$

(4) 重复2,3直到截止条件

注: 上面的例子是不断的更新迭代\({Q _i}\)和\(\theta\)。我们完全可以使用梯度上升发不断从各个方向更新\({Q _i}\)和\(\theta\)，来完成最大值的逼近。

2.3 混合高斯分布的公式推导

对比之前的内容，我们可以发现混合高斯分布的聚类问题为EM算法的一个特例。可以通过通用的EM算法来证明，下面我们来证明这一过程。

注： 这里只简单地提示计算，不展开了，因为与之前的高斯判别分析类似。
根据上一节，我们已得到E步骤的公式：

$$w _j^{(i)}={Q _i}({z^{(i)}}=j) = p({z^{(i)}}|{x^{(i)}};\theta )$$

然后对于M步骤，我们将\({Q _i}\)为一个已知值的方式对\(\theta\)进行求导，从而求得下确定的最大值，记为下一个迭代值。将最大释然函数展开记为如下函数：

$$\ell (\theta ) = \sum\limits _{i = 1}^m {\sum\limits _{j = 1}^k {{Q _i}({z^{(i)}} = j)\ln (\frac{{p({x^{(i)}},{z^{(i)}} = j;\theta )}}{{{Q _i}({z^{(i)}} = j)}})} } = \sum\limits _{i = 1}^m {\sum\limits _{j = 1}^k {w _j^{(i)}\ln (\frac{{\frac{1}{{{{(2\pi )}^{\frac{n}{2}}}|\Sigma {|^{\frac{1}{2}}}}}\exp ( - \frac{1}{2}{{({x^{(i)}} - {\mu _j})}^T}{\Sigma ^{ - 1}}({x^{(i)}} - {\mu _j})){\phi _j}}}{{w _j^{(i)}}})} } $$

然后对\(\phi\),\(\mu\),\(\Sigma\), 即可得到M步骤的更新公式。