机器学习-3.2-非监督学习之主成分分析.md

主成分分析(PCA)

严格上说PCA应该算是一种降低维度的方法，这里暂时归类为非监督学习中。

1 PCA理论简述

PCA的主要思路是将\(n\)维数据降维到\(k\)维子空间中，以滤除不需要的噪声或没有意义的特征信息。譬如我们有汽车的一组运行数据，包括专项半径、速度等。其中就一个用英里/每小时和千米/每小时描述的速度，很明显两者是呈线性关系的，只是因为舍入带来一些误差，对于这样的问题我们完全可以将这个\(n\)维数据移到\(n-1\)维子空间中。

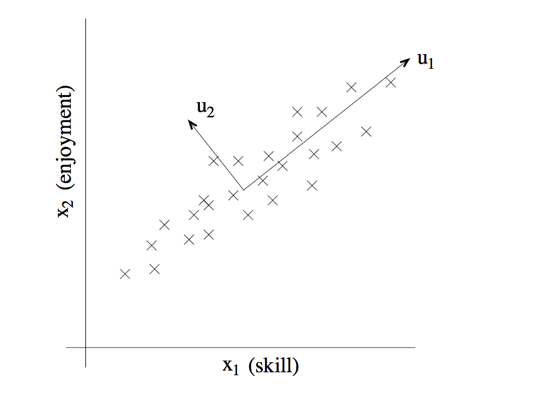
再举一个例子,对于RC直升机驾驶员的调查，\(x _1\)表示飞行员驾驶技能，\(x _2\)表示他对驾驶直升飞机的爱好程度。因为RC直升机很难驾驶，因此我们可以认为只有任务对驾驶RC直升机感兴趣的驾驶员才能学好它。因此,\(x _1\)和\(x _2\)有强相关性。如下图所示，我们可以假定一个方向\(u _1\)，用来表示\(x _1\)和\(x _2\)两个属性，仅仅在其垂直轴\(u _2\)上有少量噪声。

对数据降维之前，我们需要对数据进行初始化，主要是一个归整的过程，将均值归整为0，将方差归整为1。依次按照如下公式进行归整。

  • \(\mu = \frac{1}{m}\sum\limits _{i = 1}^m {x^{(i)}} \)
  • \({x^{(i)}}: = {x^{(i)}} - \mu \)
  • \({\sigma ^2} = \frac{1}{m}\sum\limits _{i = 1}^m {(x{(i)})2} \)
  • \({x^{(i)}}: = {x^{(i)}}/\sigma \)

归整后的数据如下，可以知道如果\(x\)在向量\(u\)的投影最大。说明\(u\)在对\(x _1\)和\(x _2\)的降维过程中带来的损失越小。

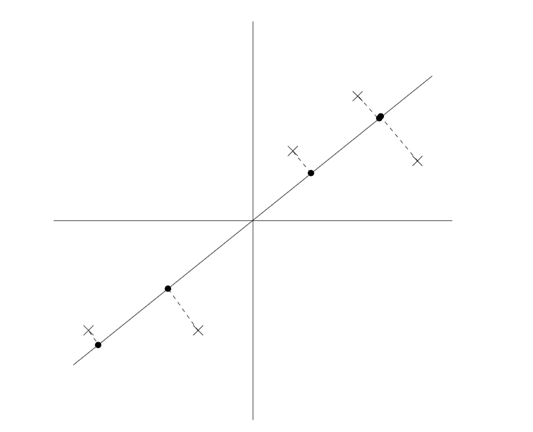
因此，可以需要保证下式最大：

$$\frac{1}{m}\sum\limits _{i = 1}^m {{{({x^{{{(i)}^T}}}u)}^2}} = \frac{1}{m}\sum\limits _{i = 1}^m {{u^T}{x^{(i)}}{x^{{{(i)}^T}}}u} = {u^T}(\frac{1}{m}\sum\limits _{i = 1}^m {{x^{(i)}}{x^{{{(i)}^T}}}} )u$$

问题也就转变为找到一组\(u\)使得，上式最大的问题。然后我们假定\(u\)为一组标准正交基，因此\(||u||=1\)。因此问题可写为如下形式：

$$\begin{gathered} & \max {u^T}(\frac{1}{m}\sum\limits _{i = 1}^m {{x^{(i)}}{x^{{{(i)}^T}}}} )u \hfill \\\ s.t.: & ||u|| = 1 \hfill \\\ \end{gathered} $$

组成其拉格朗日函数如下：

$$L(u,\lambda ) = {u^T}(\frac{1}{m}\sum\limits _{i = 1}^m {x^{(i)}x^{(i)^T}} )u - \lambda (||u|| - 1)$$

这里我们设\(\Sigma=\frac{1}{m}\sum\limits _{i = 1}^m {x{(i)}{x{(i)^T}}}\)，然后对\(u\)求导数，易得:

$${\nabla _u}L(u,\lambda ) = \sum u - \lambda u = 0$$

因此，我们知道\(\lambda\)为\(\Sigma\)的特征值，\(u\)为对应的特征向量。恰好为我们要求的向量\(u\)。得到一组新的正交基后，我们就可以映射到新的空间中了。具体如下:

$${y^{(i)}} = {(u _1^T{x^{(i)}},u _2^T{x^{(i)}},...,u _k^T{x^{(i)}})^T}$$

2. PCA的奇异值分解

由于一般为\(n*n\)的维度，因此往往是一个很大的矩阵。对于维度很大，样本数目要少于维度很多的数据，这样计算往往有不够划算。因此我们可以通过求解\(x\)的特征值的方法来求节\(\Sigma\)的特征向量。

由于求矩阵的单位特征向量，可以不考虑1/m这个系数。

假如对\(x\)进行奇异值分解，其中\(U\)和\(V\)均为酉阵，\(\Lambda\)为对角阵。另外值得注意的是酉阵的可逆矩阵与转置矩阵相同。具体分解形式如下：

$$x = U\Lambda {V^T}$$

因此可以得到：

$$\Sigma = x{x^T} = U\Lambda {V^T}V\Lambda {U^T} = U{\Lambda ^2}{U^T}$$ $$\Sigma U = {\Lambda ^2}{U^T}$$

因此可以知道\(\Sigma\)的特征向量对应着\(x\)的奇异值分解中的\(U\)。同时\(\Sigma\)的特征值为\(x\)的奇异值的平方。

3 源码实现

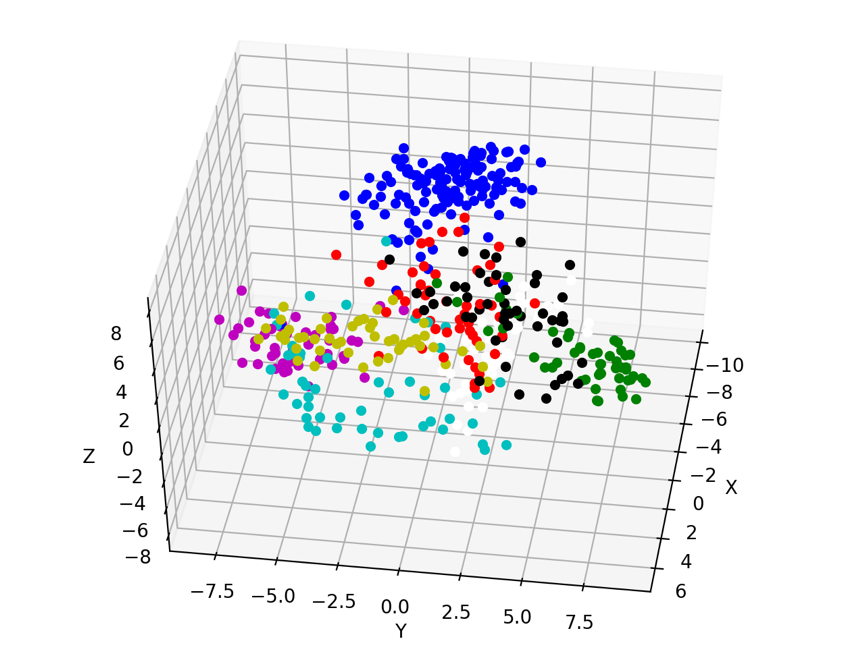
我们对k临近算法中的手写数字识别做分析。我们首先对数字映射到三维空间中，然后进行展示。然后在映射到样本数量维度的空间，实现对数字的识别。值得一提是，PCA可以将多种无法直接展示的多维数组转化为三维数据，然后更直观地进行分析。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
import numpy as np
import os
from numpy import linalg
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d, Axes3D

global g_label      # 训练集的label

def makeTrain(dir):
  dirs=os.listdir(dir)
  files = filter(lambda item:not os.path.isdir(item), dirs)
  mat = []
  label = []
  for file in files:
    arr = []
    f = open(dir+"/"+file)
    while True:
      line = f.readline()
      if not line:
        break
      for i in range(len(line)-1):        # line[len(line)]='\n'
        arr.append(float(line[i]))
    mat.append(arr)
    label.append(int(file.split("_")[0]))
  return (mat,label)

def preprocessing(trainList):
  train = np.array(trainList)
  rows = len(train)
  cols = len(train[0])
  # 使数学期望为0
  for col in range(cols):
    mean = np.mean(train[:,col])
    for row in range(rows):
      train[row][col] = train[row][col]-mean
    # 使方差为1。 如果方差小于1,任务反差为0，则不更新该行。
    # 实际上，由于手写数字已经被归整为0,1这样的二值化图像，因此这里没有修改波定性。
    var = np.var(train[:,col])
    if var > 1:
      print("hello")
      standard = np.sqrt(var)
      for row in range(rows):
        train[row][col] = train[row][col]/standard
  return train.tolist()

def lowerDimension(u3t,dir):
  # 该函数将1024维度的数据转化为3维
  dirs=os.listdir(dir)
  files = filter(lambda item:not os.path.isdir(item), dirs)
  mat = []
  label = []
  for file in files:
    arr = []
    f = open(dir+"/"+file)
    while True:
      line = f.readline()
      if not line:
        break
      for i in range(len(line)-1):        # line[len(line)]='\n'
        arr.append(float(line[i]))
    new_mat = u3t*np.mat(arr).T
    label.append(int(file.split("_")[0]))
    mat.append((np.array(new_mat.T)[0]).tolist())
  return (mat,label)         # mat为num*3的list

def show3D(g_train_3d):
  fig = plt.figure()
  ax = Axes3D(fig)
  #将数据点分成三部分画，在颜色上有区分度
  m = len(g_train_3d)
  for i in range(m):
    if g_label[i] == 0:
      ax.scatter(g_train_3d[i][0], g_train_3d[i][1], g_train_3d[i][2], c='b')
    elif g_label[i] == 1:
      ax.scatter(g_train_3d[i][0], g_train_3d[i][1], g_train_3d[i][2], c='c')
    elif g_label[i] == 2:
      ax.scatter(g_train_3d[i][0], g_train_3d[i][1], g_train_3d[i][2], c='g')
    elif g_label[i] == 3:
      ax.scatter(g_train_3d[i][0], g_train_3d[i][1], g_train_3d[i][2], c='k')
    elif g_label[i] == 4:
      ax.scatter(g_train_3d[i][0], g_train_3d[i][1], g_train_3d[i][2], c='m')
    elif g_label[i] == 5:
      ax.scatter(g_train_3d[i][0], g_train_3d[i][1], g_train_3d[i][2], c='r')
    elif g_label[i] == 6:
      ax.scatter(g_train_3d[i][0], g_train_3d[i][1], g_train_3d[i][2], c='w')
    elif g_label[i] == 7:
      ax.scatter(g_train_3d[i][0], g_train_3d[i][1], g_train_3d[i][2], c='y')
#    elif g_label[i] == 8:
#      ax.scatter(g_train_3d[i][0], g_train_3d[i][1], g_train_3d[i][2], c='b', depthshade=False)
#    elif g_label[i] == 9:
#      ax.scatter(g_train_3d[i][0], g_train_3d[i][1], g_train_3d[i][2], c='c', depthshade=False)
  ax.set_zlabel('Z') #坐标轴
  ax.set_ylabel('Y')
  ax.set_xlabel('X')
  plt.show()

def test(ukt, train_3d, dir):
  test_kd,test_label = lowerDimension(ukt, dir)
  testN = len(test_kd)
  right=0
  wrong=0
  for i in range(testN):
    label = classify(np.array(test_kd[i]),np.array(train_3d),10)
    if str(test_label[i]) == label:
      right = right + 1
    else:
      wrong = wrong + 1
  print("right=", right, ", wrong=", wrong)

def classify(vec,train_kd,k):
  # 计算各个训练数据与测试数据的距离
  m = len(g_label)
  dis = []
  for i in range(m):
    dis.append([linalg.norm(vec-train_kd[i]),g_label[i]])
  dis = sorted(dis, key=lambda v:v[0])
  # 计算相似度最高的k个值，这里写入map做累积
  dic = {}
  for j in range(k):
    if not str(dis[j][1]) in dic:
      dic[str(dis[j][1])]=1
    else:
      dic[str(dis[j][1])]=dic[str(dis[j][1])]+1
  return max(dic.items(), key=lambda x: x[1])[0]

if __name__=="__main__":
  # 1 预处理
  # 这里为了显示降低维度在训练样本中的作用，仅仅是用了300个样本
  (train,g_label) = makeTrain("/Users/zcy/Desktop/study/git/mlearning/res/trainingDigits1")
  # 进行预处理操作，将均值设置为0，将方差归整为1
  train_processed = preprocessing(train)

  # 2 降低维度
  # 首先计算x的奇异值
  train_mat = np.mat(train_processed)
  train_mat = train_mat.T               # 转化为n*m 1024*200
  U,sigma,VT = linalg.svd(train_mat)      # U的维度为n*n 即1024*1024. sigma为m*1. vt为300*300
  u3=U[np.ix_(np.arange(1024), np.arange(3))]      # 提取对应最高特征值最高的三个方向,u3的维度为1024*3
  # 将1024维的数字图像降低维度到三维向量
  train_3d,_ = lowerDimension(u3.T,"/Users/zcy/Desktop/study/git/mlearning/res/trainingDigits1")
  train_kd,_ = lowerDimension(U.T,"/Users/zcy/Desktop/study/git/mlearning/res/trainingDigits1")

  # 3 展示3维下的模型信息
  #show3D(train_3d)

  # 4 使用k邻域验证测试样本
  #test(u3.T, train_3d, "/Users/zcy/Desktop/study/git/mlearning/res/testDigits1")
  test(U.T,train_kd,"/Users/zcy/Desktop/study/git/mlearning/res/testDigits1")

500个测试样本中，有27个识别错误，具体识别率为94.6%。这与未使用PCA降维的完全一致。该例子似乎尚未体现到PCA有什么优势，以后有机会在分析。当然如果映射到三维空间，识别率仅仅为75.2%，因此不要过度降维。下面是一个展示到部分数据的三维图。

考虑到颜色，图片只显示部分类别数据。

4 参考文献

  • cs229-note10
  • 机器学习实战