本文侧重于如何从依据理论指导实践，在不适用任何第三方库的情况下实现ErasuceCode算法。本文仅会对用到的理论做简单的解释并标记引用，不会做详细解释。因此阅读本文前请熟读文献[1]第四章内容。
本文代码存储于https://github.com/zhengchenyu/SimpleErasureCode, SimpleErasureCode只是为了便于方便理解，为了保持与文章保持一致，因此没有优化。部分关键流程文章中会有链接到对应的代码。

EC算法在存储领域和通信领域都有广泛的应用。在分布式存储领域，为了避免机器宕机，需要存储3份冗余副本，这3台机器最多允许2台宕机。如果使用EC RS-6-3的话，可以实现使用9个副本冗余6份数据，这9台机器最多允许3台宕机，而且存储量却减少了一半。分布式存储使用EC在几乎不降低可用性的前提下，降低了冗余副本数，大大节约了存储资源。

实现EC算法是检验是否理解EC算法的重要手段。对EC算法的理解对工程上也有很大的帮助，笔者实现EC算法的初衷也是为了解决HADOOP-19180提出的问题。

1 算法概述

本文以RS-6-3算法为例, 存在6个数据块和3个校验块。EC算法的两个基本问题:

  • 如何通过数据块生成校验块?
  • 如何通过部分数据块和校验块恢复丢失的数据块?

1.1 生成校验块

生成校验块即编码过程(encode)。对6个数据块依次取出byte, 即d0,d1,d2,d3,d4,d5。如下图所示，用编码矩阵(encodeMatrix)乘以对应的数据块,即得到原有的数据d0,d1,d2,d3,d4,d5和对应的校验字节c0,c1,c2(编码过程)。对数据块的所有字节依次执行上述的操作就得到了校验块。

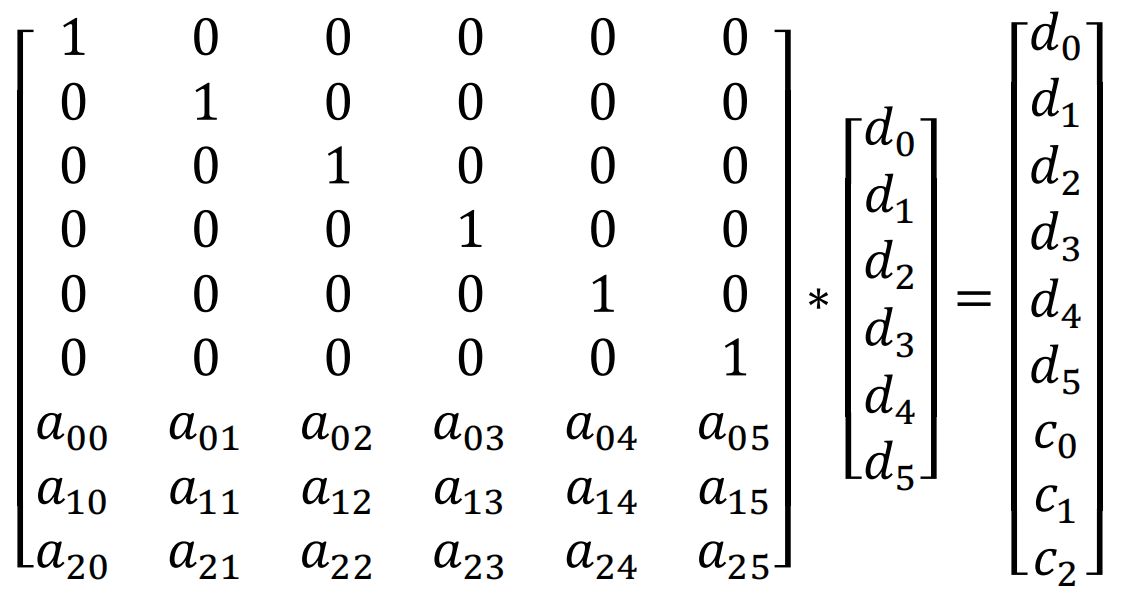
1.2 恢复数据块

恢复数据块的过程即解码过程(decode)。假如d2,d3,d4丢失了，我们需要通过d0,d1,d5,c0,c1,c2恢复d2,d3,d4。在上面公式中删除对应的行，公式中用d2?,d3?,d4?表示数据块丢失。有如下公式:

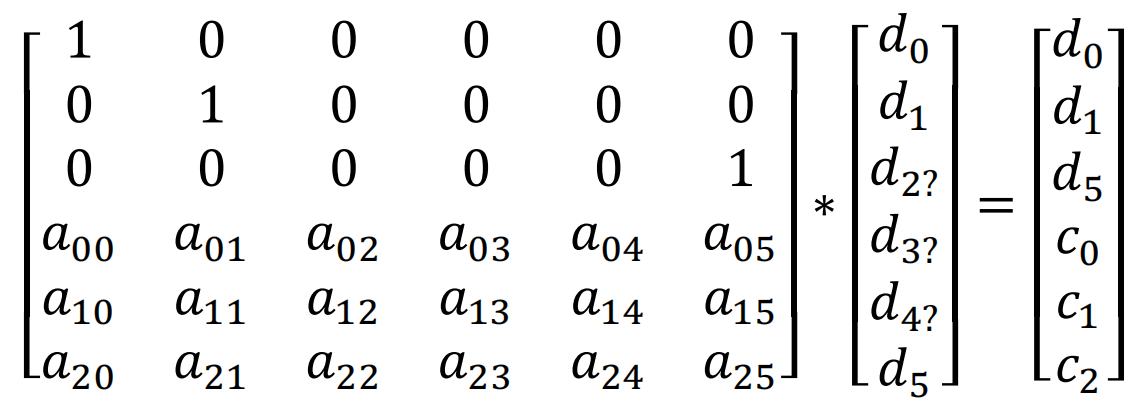
对上面的公式两侧都乘以裁剪后的矩阵的逆矩阵，这个逆矩阵即解码矩阵(decodeMatrix)。可以得到如下的公式:

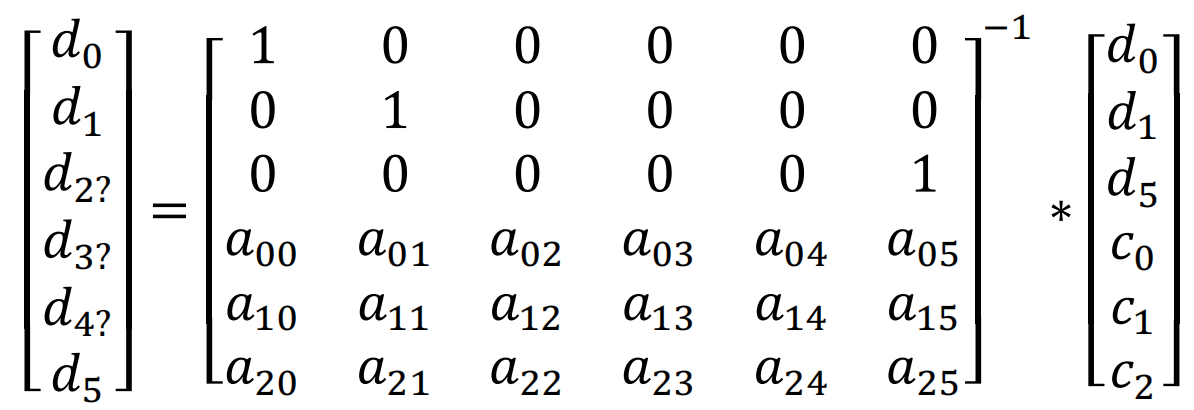
得到解码矩阵后其实计算过程与编码类似，只是输入为为d0,d1,d5,c0,c1,c2，输出为d0,d1,d2,d3,d4,d5。

2 关于矩阵

上一章节已经介绍了EC编解码的基本过程，但工程实现上让然会有一些问题需要解决。这一小节主要介绍一下关于矩阵方面的问题。

2.1 如何选择矩阵

根据第一小节的分析，编码矩阵是一个9 * 6的矩阵。而解码矩阵是在编码矩阵的基础上删除任意三行，然后再求逆的。因此我们定义编码矩阵的时候要保证，对于这个9 * 6的编码矩阵，任意删除三行得到的6 * 6的矩阵是一个可逆矩阵。
为了便于计算，编码矩阵的上半部分使用的是6 * 6 的单位矩阵，单位矩阵是可逆的，是满足条件的。接下来就是给下半部分的3 * 6的找到合理的矩阵。本文使用的是范德蒙矩阵。

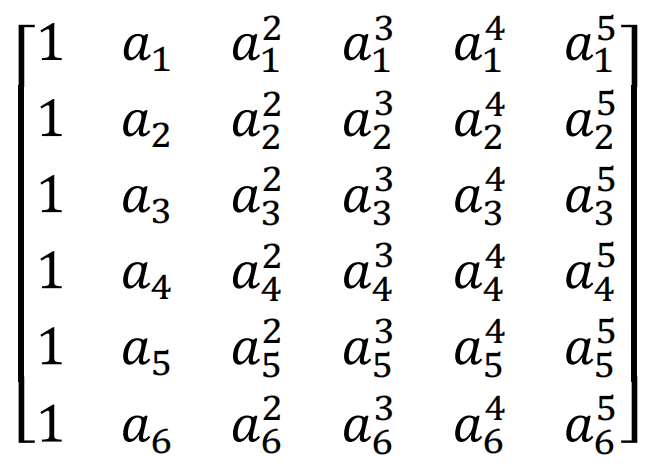
由于MathType不支持新版Mac, 而且markdown经常因为调整不好乱码，这里的共识还是贴图吧…

如下为范德蒙矩阵的行列式:

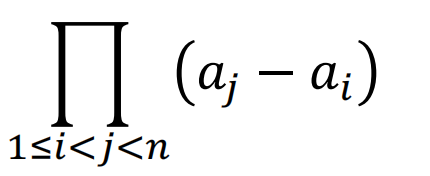
只要ai各不相等且不为0，则范德蒙矩阵一定可逆，意味着任意挑出3行向量，一定是线性无关的。那我们就挑出前三行，令a1=1,a2=2,a3=3，便可以得到如下编码矩阵:

前面已经说明了前6行向量是互为线性无关，后3行向量也是互为线性无关的。如果在前6行中选取n行，在后三行中去6-n行，那么这6行向量还是线性无关的吗？假设n为5，由于后三行的没有元素为0，因此肯定是缺一个维度来保证线性相关。如果n为4和3也是同样的道理。因此这个9 * 6的矩阵随意挑出6行组成的6 * 6阶矩阵一定是可逆的。

2.2 高斯消元求逆

本文使用了容易理解的高斯消元法求逆(inverse)。假设当前6 * 6矩阵为A, 在右侧再拼接6 * 6的单位矩阵E，得到矩阵[A | E]。如果使用A-1乘以这个矩阵，会得到[E|A-1]。这样我们只需将A矩阵转化为单元矩阵，E矩阵自然就变成了A-1。(高斯消元求逆)
对每一行行依次执行如下的过程:

  • (1) 对第i行, 找到第i行第i列的值。(Step1)
  • (2) 然后计算该值的乘法逆元。然后让该行的每个元素均乘以这个乘法逆元。(Step2)
  • (3) 对其他行j，使用第i行经过线性变换将地地j行第i列的值消为0。

经过这三步变换为，对于第i列，有且只有地i行的数据为1，其他均为0。对每一行均执行如下操作，左侧变得到了单位矩阵，右侧的结果也即A-1。

对于有理数域中，乘以乘法逆元即除法，加上加法逆元即减法。这样描述对伽罗华域中的数学运算的描述更准确。

对于第0行计算的过程如下，其他行同理。

还有一种特殊的情况，譬如上述矩阵如果处理第2行。第2行和第2列的元素值为0，0是没有乘法逆元的。所以这时候就需要找到第2行下面的行中第2列不为0的情况，把该行加到第2行上，这样可以保证算法可运行(setup for step1)。其实移位可能更高效，但是为了便于理解，采用这样的方式。

3 伽罗华域

矩阵运算还存在一个问题，数据都是byte存储的，是一个0-255的数值。经过有理数运算后，数值是很容易越界的。因此我们需要一套新的计算体系同时满足以下两个条件:

  • 该算法体系的值和计算得到的值只能是在有限的集合范围内，即不越界。
  • 可以通过有限的运算恢复得到原有值，即可解码。

这就需要使用伽罗华有限域。伽罗华有限域可以保证任何计算得到的结果均在有限集合内，这满足了不越界的要求。另外伽罗华有限域的运算都有对应的逆运算。譬如对a，如果a乘以b，再乘以b的加法逆元，结果仍然是a。这满足了可解码的要求。

这里为了便于理解先简单的介绍GF(7)，然后再解释实际使用的GF(28)。

本章并没有详细的证明。譬如将7扩张到无穷大的质数的时候，如何证明相应的定理为什么成立。事实上笔者也不知道，参考文献上也没有严谨的证明。也只是简单的说明了合数不能作为模数。但对于工程上有限的集合内，很容易通过穷举法来证明算法的可行性。

3.1 GF(7)

首先给出如下定义:

  • 加法逆元: 给定x，如果存在x’，使得x+x’=x’+x=0，则称x’是x的加法逆元。
  • 乘法逆元: 给定x，如果存在x’，使得x * x’=x’ * x=e，则称x’为x的乘法逆元。其中e为该群的单位元。对于GF(7)，e为1。

我们定义一种新的运算，即模7运算。对于加法和乘法运算，我们会将结果然后模7。譬如, 8 + 3 = 11 mod 7 = 4。8 * 3 = 24 mod 7 = 3。
对于加法逆元和乘法逆元，根据定义我们可以穷举加法和乘法计算，根据结果得到对应的逆元。譬如, 4 + 3 = 7 mod 7 = 0，我们就说4和3互为加法逆元。2 * 4 = 8 mod 7 = 1，我们就说2和4互为乘法逆元。
下表穷举了GF7的所有加法和乘法运算，根据码表也得到了GF(7)下所有元素对应的加法逆元和乘法逆元。

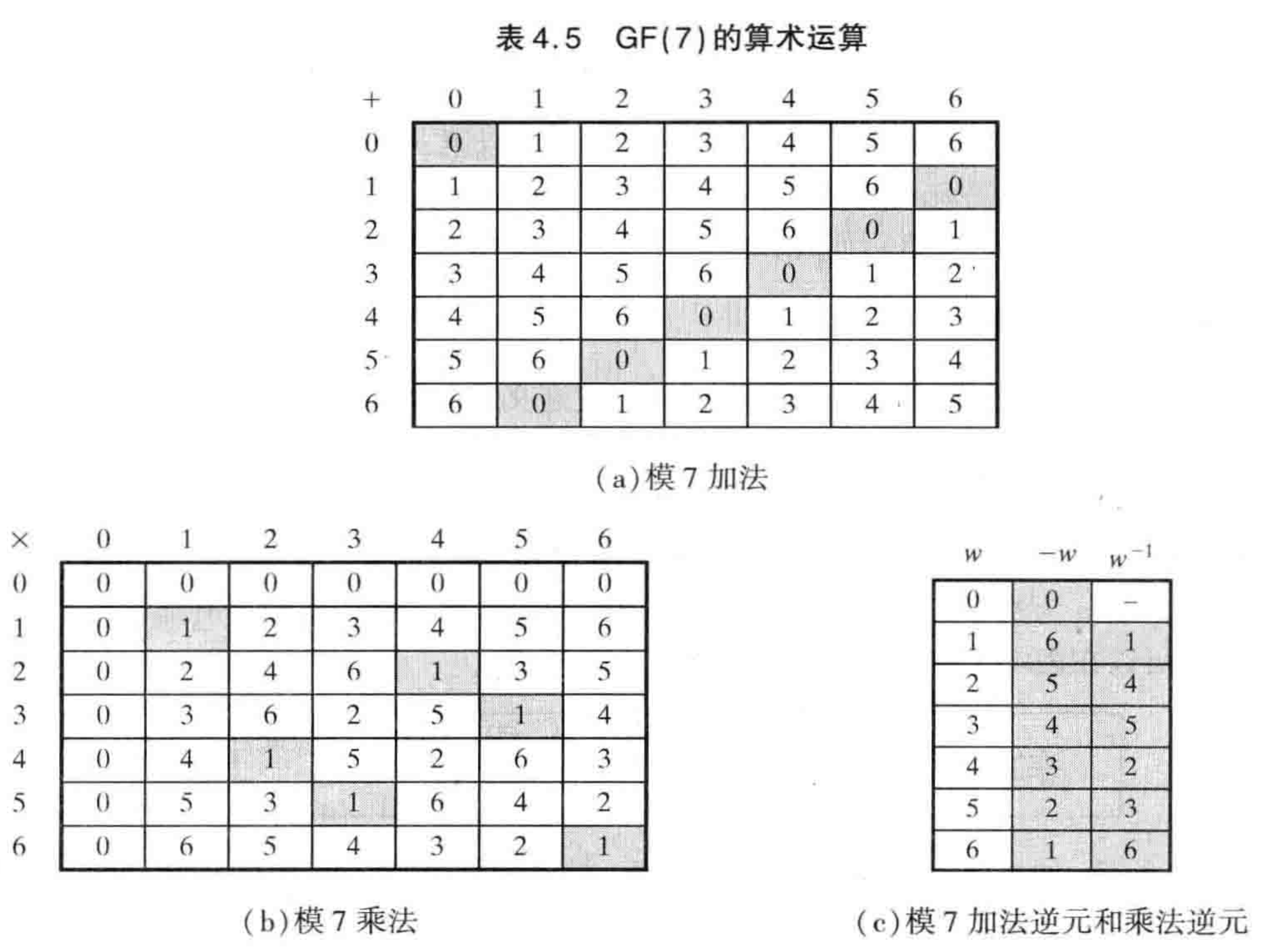
来看下是否满足我们的要求，不越界在定义上就满足了。可解码的特点，我们随机指定数组假设为5，用5乘以3在乘以3的乘法逆元5, 得到的值为5 * 3 * 5 = 75 mod 1 = 5。事实上根据乘法交换律很容易证明这个。对于加法逆元的解码同理。

3.2 GF(28)

3.2.1 基本原理

实际的数字存储的值是0-255, 那么是否意味着我们可以直接使用GF(256)呢? 答案是不可以的。因为256是合数，譬如16 * 16 = 256 mod 256 = 0，那么16就不存在乘法逆元，也就难以进行边界吗。
因此需要引入多项式的运算，且要求同指数幂下遵循GF(2)。模数为不可约多项式。对于不可约多项式a, 无法找到两个不为1的多项式b和c使得b * c = a。可以使用穷举法得到每个多项式的加法逆元和乘法逆元。事实上只要集合内的每个元素都有1对1对应的乘法逆元，就可以满足我们的要求。文献1的表4.6也通过穷举证明了GF(23)的有效性。
多项式的计算与对byte的编码有什么关系呢？由于多项式的同指数幂是GF(2)，也就意味着对于多项式a0 + a1x + a2x2 + a3x3 + a4x4 + a5x5 + a6x6 + a7x7 ，ai 为0和1。如果a0为第0位，a1为第1位，依次类推，这组系数就是一个byte。这样就把要存储的byte与多项式运算结合了。

3.2.2 计算

本章主要介绍如何计算GF(28)。对于加法和乘法，我们直接使用多项式运算。对于加法逆元和乘法逆元，我们穷举加法和乘法运算，然后通过码表来得到加法和乘法逆元。
本文的算法的不可约多项式为x8 + x4+ x3 + 1。
f(x) = x6 + x4+ x2 + x + 1, g(x) = x7 + x + 1
对于加法, 指数幂执行GF(2)运算，G(2)运算实际上就是异或。得到f(x)+g(x)= x7 + x6 +x4+ x2 + 1。实际可以理解为f(x)对应的二进制0b01010111与g(x)对应的二进制0b10000011进行按位的异或计算。(GF(28))
对于乘法, 先考虑h(x) = a0 + a1x + a2x2 + a3x3 + a4x4 + a5x5 + a6x6 + a7x7, 计算 h(x) * x = (a0x + a1x2 + a2x3 + a3x4 + a4x5 + a5x6 + a6x7 + a7x8 ) mod (x8 + x4+ x3 + x + 1)。存在两种情况

  • (1) a7 等于 0
    那么该式已经不可约，因此h(x) * x= a0x + a1x2 + a2x3 + a3x4 + a4x5 + a5x6 + a6x7。也就意味着[a7a6a5a4a3a2a1a0] * [00000010] = [a6a5a4a3a2a1a00]，即向左移动一位。(a7 等于 0)
  • (1) a7 不等于0
    h(x) * x = (a0x + a1x2 + a2x3 + a3x4 + a4x5 + a5x6 + a6x7 + x8) mod (x8 + x4+ x3 +x+ 1) = a0x + a1x2 + a2x3 + a3x4 + a4x5 + a5x6 + a6x7 + x8 - x8 - x4 - x3 -1 = 1 + (a0+1)x + a1x2 + (a2+1)x3 + (a3+1)x4 + a4x5 + a5x6 + a6x7。以为意味着[a7a6a5a4a3a2a1a0] * [00000010] = [a6a5a4a3a2a1a00] ^ [00011011]。即左移一位后，在于不包含最高位系统的字节进行异或。(a7 不等于 0)

这里减法为加法逆元，对于GF(2)，加法逆元就是自己。

f(x) * g(x) = ((x6 + x4+ x2 + x + 1) * ( x7 + x + 1))。我们可以把他分解为一下三个运算之和。

  • (1) (x6 + x4+ x2 + x + 1) * x7
  • (2) (x6 + x4+ x2 + x + 1) * x
  • (3) (x6 + x4+ x2 + x + 1) * 1
    对于(2)在前面已经介绍了，对于(3)实质上不用计算。对于(1), 我们可以使用(2)的计算方法进行递归计算(fxxn)。然后分别计算的三个值进行相加便得到了最终的结果(_mul)。

至此，ErasureCode算法的所有问题都已经得到了解释。本文以自顶向下的方式描述了如何从理论到实践来实现ErasureCode算法。完整的代码见SimpleErasureCode。

参考文献: